题目内容
 已知:如图,AB:BC:CD=1:3:2,M为AB的中点,N为CD的中点,且MN=9,求AD的长.
已知:如图,AB:BC:CD=1:3:2,M为AB的中点,N为CD的中点,且MN=9,求AD的长.考点:两点间的距离
专题:
分析:设每份为x,则AB=x,BC=3x,CD=2x,由中点的定义就可以得出MB=0.5x,CN=x,由MN=9建立方程求出其解即可;
解答:解:设每份为x,则AB=x,BC=3x,CD=2x.
∵M为AB的中点,N为CD的中点,
∴MB=0.5x,CN=x.
∵MN=MB+BC+CN=9,
∴0.5x+3x+x=9,
∴x=2,
∴AB=2,BC=6,CD=4,
∴AD=AB+BC+CD=12.
答:AD的长为12.
∵M为AB的中点,N为CD的中点,
∴MB=0.5x,CN=x.
∵MN=MB+BC+CN=9,
∴0.5x+3x+x=9,
∴x=2,
∴AB=2,BC=6,CD=4,
∴AD=AB+BC+CD=12.
答:AD的长为12.
点评:本题考查了中点的性质的运用,两点间的距离的运用,比例问题的运用.解答时由比例问题设每份为x表示出MN的长建立方程是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在直线l上顺次取A,B,C,D四点,并且使AB:BC:CD=2:3:4,如果AB中点M与CD中点N的距离是12cm,那么CD的长是( )
| A、4cm | B、6cm |
| C、8cm | D、24cm |
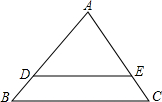 如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则
如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则| DE |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,张雨同学想出了一个测量池塘两端A、B长度的方法:过点A、B引两条直线AC、BC相交于点C,在BC上取点E、G,使BE=CG,再别分别过点E、G作EF∥AB、GH∥AB交AC于点F、H,测得EF=11m,GH=5m,她就得出了结论:池塘的宽AB为16m,你认为她说的对吗?请说明理由.
如图,张雨同学想出了一个测量池塘两端A、B长度的方法:过点A、B引两条直线AC、BC相交于点C,在BC上取点E、G,使BE=CG,再别分别过点E、G作EF∥AB、GH∥AB交AC于点F、H,测得EF=11m,GH=5m,她就得出了结论:池塘的宽AB为16m,你认为她说的对吗?请说明理由. 如图,点C、D是线段AB上两点,AB=8cm,CD=3cm,M,N分别为AC,BD的中点,
如图,点C、D是线段AB上两点,AB=8cm,CD=3cm,M,N分别为AC,BD的中点,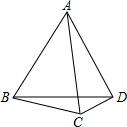 如图,在△ABC中,AB=AC,∠ABC>60°,∠ABD=60°,且∠ADB=90°-
如图,在△ABC中,AB=AC,∠ABC>60°,∠ABD=60°,且∠ADB=90°-