题目内容
已知a+b=5，a-b=3．
（1）求a2+b2的值；
（2）已知三个代数式：①a2-b2，②a2+2ab+b2，③a2-2ab+b2，从中任意选择两个代数式造成分式，然后进行化简并求值．
（1）求a2+b2的值；
（2）已知三个代数式：①a2-b2，②a2+2ab+b2，③a2-2ab+b2，从中任意选择两个代数式造成分式，然后进行化简并求值．
考点：分式的化简求值,完全平方公式
专题：开放型
分析：（1）把已知两式分别平方，利用完全平方公式化简，相加即可求出所求式子的值；
（2）选①②找组成分式，约分后把a+b与a-b的值代入计算即可求出值．
（2）选①②找组成分式，约分后把a+b与a-b的值代入计算即可求出值．
解答：解：（1）把a+b=5两边平方得：（a+b）2=a2+b2+2ab=25①，
把a-b=3两边平方得：（a-b）2=a2+b2-2ab=9②，
①+②得：2（a2+b2）=34，即a2+b2=17；
（2）若选①②，组成分式为
=
=
=
．
把a-b=3两边平方得：（a-b）2=a2+b2-2ab=9②，
①+②得：2（a2+b2）=34，即a2+b2=17；
（2）若选①②，组成分式为
| a2-b2 |
| a2+2ab+b2 |
| (a+b)(a-b) |
| (a+b)2 |
| a-b |
| a+b |
| 3 |
| 5 |
点评：此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
设⊙O1和⊙O2的半径分别是r1，r2，且r1，r2是关于x的方程x2+ax+1=0的两个根．若⊙O1和⊙O2是等圆，则a的值是（ ）
| A、a＞2或a＜-2 | B、a=±2 |
| C、a=2 | D、a=-2 |
如图，张雨同学想出了一个测量池塘两端A、B长度的方法：过点A、B引两条直线AC、BC相交于点C，在BC上取点E、G，使BE=CG，再别分别过点E、G作EF∥AB、GH∥AB交AC于点F、H，测得EF=11m，GH=5m，她就得出了结论：池塘的宽AB为16m，你认为她说的对吗？请说明理由．
如图，点C是线段AB的一个三等分点，D在CB上，CD：DB=9：1，且CD-AC=2，求线段AB的长．
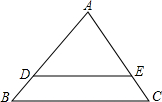如图，平行于BC的直线DE把△ABC分成的两部分面积相等，则| DE |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|