题目内容
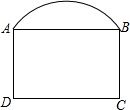如图，工厂大门由弧线AB和矩形ABCD组成， |
| AB |
|
| AB |
考点：垂径定理的应用,勾股定理
专题：
分析：作AB的垂直平分线交AB于点E，交
于点H，截取OH=5m，连接OA，则OA=oh5m，即点O为
所在圆的圆心，根据DC=6m可知AB=6m，由垂径定理求出AE的长，再由勾股定理求出OE的长，进而可得出HE的长，由此得出结论．
|
| AB |
|
| AB |
解答：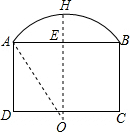
解：作AB的垂直平分线交AB于点E，交
于点H，截取OH=5m，连接OA，则OA=OH5m，即点O为
所在圆的圆心，
∵四边形ABCD是矩形，DC=6m，
∴AB=6m，
∴AE=
AB=3m，
∴OE=
=
=4m，
∴EH=5-4=1m，
∴
的中点到地面CD的距离=EH+AD=1+3.7=4.7m．
故答案为：4.7．
解：作AB的垂直平分线交AB于点E，交 |
| AB |
|
| AB |
∵四边形ABCD是矩形，DC=6m，
∴AB=6m，
∴AE=
| 1 |
| 2 |
∴OE=
| OA2-AE2 |
| 52-32 |
∴EH=5-4=1m，
∴
|
| AB |
故答案为：4.7．
点评：本题考查的是垂径定理的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
如图，点C、D是线段AB上两点，AB=8cm，CD=3cm，M，N分别为AC，BD的中点，在直线l上顺次取A，B，C，D四点，并且使AB：BC：CD=2：3：4，如果AB中点M与CD中点N的距离是12cm，那么CD的长是（ ）
| A、4cm | B、6cm |
| C、8cm | D、24cm |
下列说法中正确的是（ ）
| A、两点之间，直线最短 |
| B、线段MN就是M、N两点之间的距离 |
| C、在连接两点的所有线中，最短线的长度就是这两点之间的距离 |
| D、从广州到北京火车行走的路程就是广州到北京的距离 |
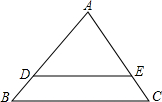如图，平行于BC的直线DE把△ABC分成的两部分面积相等，则| DE |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在Rt△AOB中，OA=OB=3，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线PQ的最小值为
如图，AD为△ABC的角平分线，BF⊥AD的延长线于点F，AM⊥AD于A交BC的延长线于M，FC的延长线交AM于E．求证：AE=EM．已知二次函数y=x2+3x+m（m为常数）的图象与x轴有两个交点，其中一个交点为（-1，0），则另一个交点是（ ）
| A、（1，0） |
| B、（2，0） |
| C、（-2，0） |
| D、（-3，0） |