题目内容
已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=CG，连接BG并延长交DE于F．
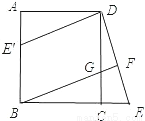
（1）求证：△BCG≌△DCE；
（2）将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形，并说明理由。
（1）答案见解析；（2）答案见解析
【解析】试题分析：（1）由正方形ABCD，得BC=CD，∠BCD=∠DCE=90°，又CG=CE，所以△BCG≌△DCE（SAS）．
（2）由（1）得BG=DE，又由旋转的性质知AE′=CE=CG，所以BE′=DG，从而证得四边形E′BGD为平行四边形．
（1）证明：∵四边形ABCD是正方形，
∴BC=CD，∠BCD=90°．
∵∠...
工人小王4月份计划生产零件270个，前 10天平均每天生产5个，后来改进技术，提前3天超额完成任务．设小王10天之后平均每天生产零件x个，请你试着写出x所满足的关系式．
50＋（20－3）x＞270
【解析】试题分析：首先设小王10天之后平均每天生产零件x个，利用4月份计划生产零件270个，改进技术后提前3天超额完成任务，进而得出不等式即可．
试题解析：设小王10天之后平均每天生产零件x个，根据题意得
50+（20-3）x＞270． 对于下列命题：（1）关于某一直线成轴对称的两个三角形全等；（2）等腰三角形的对称轴是顶角的平分线；（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点；（4）如果两个三角形全等，那么它们关于某直线成轴对称。其中真命题的个数为
A、0 B、1 C、2 D、3
C
【解析】
试题分析：根据平面图形的基本概念依次分析各小题即可作出判断.
（1）关于某一直线成轴对称的两个三角形全等，（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点，均为真命题；
（2）等腰三角形的对称轴是顶角的平分线所在的直线，（4）如果两个三角形全等，它们可能是平移或旋转构成的，均为假命题；
故选C. 下面说法中正确的是( )
A. 设A、B关于直线MN对称，则AB垂直平分MN.
B. 如果△ABC≌△DNF,则一定存在一条直线MN，使△ABC与△DNF关于MN 对称.
C. 如果一个三角形是轴对称图形，且对称轴不止一条，则它是等边三角形.
D. 两个图形关于MN对称，则这两个图形分别在MN的两侧.
C
【解析】A中应该是直线MN垂直平分线段AB，故错误；
B因为成轴对称的两个图形一定全等，但全等形不一定是轴对称图形，故错误；
C因为等边三角形是轴对称图形，且有3条对称轴，故正确；
D中错在这两个图形不一定要在直线两侧，同侧也可以有，如下图，故错误.
故选C. 下列说法错误的是( )
A. 等边三角形是轴对称图形
B. 轴对称图形的对应边相等,对应角相等
C. 成轴对称的两条线段必在对称轴一侧
D. 成轴对称的两个图形对应点的连线被对称轴垂直平分
C
【解析】A. 由等边三角形的性质知,等边三角形是轴对称图形,正确;
B. 由轴对称的性质知,轴对称图形的对应边相等,对应角相等,正确;
C. 成轴对称的两条线段必在对称轴两侧,故错误;
D. 由轴对称的性质知,成轴对称的两个图形对应点的连线被对称轴垂直平分,正确;
故选C. 用边长为4cm，5cm，6cm的两个全等三角形一共能拼成__________个平行四边形．
3
【解析】【解析】
如图所示：
共6个四边形，其中有3个平行四边形．
故答案为：3． 在下列条件中，不能确定四边形ABCD为平行四边形的是（ ）
A. ∠A=∠C，∠B=∠D B. ∠A=∠B=∠C=90°
C. ∠A+∠B=180°，∠B+∠C=180° D. ∠A+∠B=180°，∠C+∠D=180°
D
【解析】试题分析：A．∠A=∠C，∠B=∠D，能判定四边形ABCD是平行四边形；
B．∠A=∠B=∠C=90°，能判定四边形ABCD是平行四边形；
C．∠A+∠B=180°，∠B+∠C=180°，能判定四边形ABCD是平行四边形；
D．∠A+∠B=180°，∠C+∠D=180°，不能判定四边形ABCD是平行四边形．
故选D． 小明投掷一枚质地均匀的骰子,前三次投出的朝上的数字都是6,则第4次投出的朝上的数字( )
A. 按照小明的运气来看,一定还是6
B. 前三次已经是6了,这次一定不是6
C. 按照小明的运气来看,是6的可能性最大
D. 是6的可能性与是1~5中任意一个数字的可能性相同
D
【解析】要求可能性的大小，只需求出各自所占的比例大小即可．
【解析】
一枚普通的骰子共有1、2、3、4、5、6六个数字，每一个数字朝上的可能性都相等，
所以第4次投出的朝上数字是6的可能性与是1～5中任意一个数字的可能性相同．
故选D． 
___________
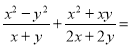【解析】试题分析：原式＝
＝
＝．
故答案为．