题目内容
工人小王4月份计划生产零件270个，前 10天平均每天生产5个，后来改进技术，提前3天超额完成任务．设小王10天之后平均每天生产零件x个，请你试着写出x所满足的关系式．
50＋（20－3）x＞270
【解析】试题分析：首先设小王10天之后平均每天生产零件x个，利用4月份计划生产零件270个，改进技术后提前3天超额完成任务，进而得出不等式即可．
试题解析：设小王10天之后平均每天生产零件x个，根据题意得
50+（20-3）x＞270．
练习册系列答案
每课必练系列答案
相关题目
先化简，后求值：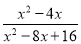 
，其中x=5．
5
【解析】原式=,
把x=5代入得,原式=5. 已知：如图，AB∥CD，求图形中的x的值．
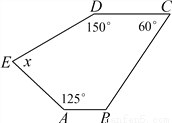
x＝85°
【解析】试题分析：先根据平行线的性质求得∠B的度数，再利用多边形的内角和定理进行求解即可.
试题解析：∵AB∥CD，∠C=60°，
∴∠B=180°-60°=120°，
∴（5-2）×180°=x+150°+125°+60°+120°，
∴x=85°． 如图，△ABC的中线BE，CF相交于点G，P、Q分别是BG、CG的中点．
(1)求证：四边形EFPQ是平行四边形；
(2)请直接写出BG与GE的数量关系.(不要求证明)．
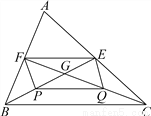
（1）证明见解析；（2）BG＝2GE.
【解析】试题分析：（1）根据BE，CF是△ABC的中线可得EF是△ABC的中位线，P，Q分别是BG，CG的中点可得PQ是△BCG的中位线，根据三角形中位线定理可得EF∥BC且EF=BC，PQ∥BC且PQ=BC，进而可得EF∥PQ且EF=PQ，根据一组对边平行且相等的四边形是平行四边形可得结论；
（2）根据平行四边形的性质可得GE=GP，再根据P是... 在△ABC中，点D、E分别是边AB、AC的中点，那么△ADE的面积与△ABC的面积的比是______.
1∶4
【解析】如图，∵AD=DB，AE=EC，
∴DE∥BC．DE=BC，
∴△ADE∽△ABC，
∴，
故答案为． 用适当的符号表示下列关系：
（l）a的2倍比a与3的和小； (2)y的一半与5的差是非负数；
（3）x的3倍与1的和小于x的2倍与5的差．
（1）2a＜a+3；（2）y-5≥0；（3）3x＋1＜ 2x－5
【解析】试题分析：（1）首先表示出a的2倍为2a，再表示a与3的和a+3，再利用不等式表示即可；
（2）首先表示y的一半为y，再表示与5的差为y-5，然后表示非负数即可；
（3）x的3倍与1的和表示为3x+1，x的2倍与5的差表示为2x-5，然后再抓住关键词“小于”列出不等式即可．
试题解析：（1）a的2倍为... 如果a+b<0，且b>0，那么a，b，－a，－b的大小关系为（ ）.
A. a<b<－a<－b
B. －b<a<－a<b
C. a<－b<－a<b
D. a<－b<b<－a
D
【解析】∵a+b<0，且b>0，
∴a<0，|a|>b，a 若一个三角形是轴对称图形，则这个三角形一定是( ）
A. 等边三角形 B. 不等边三角形 C. 等腰三角形 D. 等腰直角三角形
C
【解析】根据轴对称图形的性质即可得出答案.
A等边三角形一定是轴对称图形，但轴对称三角形不一定是等边三角形；
B不等边三角形一定不是轴对称图形；
C等腰三角形一定是轴对称三角形；
D等腰直角三角形一定是轴对称图形，但是轴对称三角形不一定是等腰直角三角形.故选C. 已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=CG，连接BG并延长交DE于F．
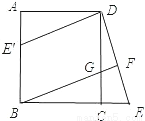
（1）求证：△BCG≌△DCE；
（2）将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形，并说明理由。
（1）答案见解析；（2）答案见解析
【解析】试题分析：（1）由正方形ABCD，得BC=CD，∠BCD=∠DCE=90°，又CG=CE，所以△BCG≌△DCE（SAS）．
（2）由（1）得BG=DE，又由旋转的性质知AE′=CE=CG，所以BE′=DG，从而证得四边形E′BGD为平行四边形．
（1）证明：∵四边形ABCD是正方形，
∴BC=CD，∠BCD=90°．
∵∠...