题目内容
在下列条件中，不能确定四边形ABCD为平行四边形的是（ ）
A. ∠A=∠C，∠B=∠D B. ∠A=∠B=∠C=90°
C. ∠A+∠B=180°，∠B+∠C=180° D. ∠A+∠B=180°，∠C+∠D=180°
D
【解析】试题分析：A．∠A=∠C，∠B=∠D，能判定四边形ABCD是平行四边形；
B．∠A=∠B=∠C=90°，能判定四边形ABCD是平行四边形；
C．∠A+∠B=180°，∠B+∠C=180°，能判定四边形ABCD是平行四边形；
D．∠A+∠B=180°，∠C+∠D=180°，不能判定四边形ABCD是平行四边形．
故选D．
练习册系列答案
相关题目
如果a+b<0，且b>0，那么a，b，－a，－b的大小关系为（ ）.
A. a<b<－a<－b
B. －b<a<－a<b
C. a<－b<－a<b
D. a<－b<b<－a
D
【解析】∵a+b<0，且b>0，
∴a<0，|a|>b，a 在等腰△ABC中，AB＝AC，O为不同于A的一点，且OB＝OC，则直线AO与底边BC的关系为
A、平行 B、垂直且平分 C、斜交 D、垂直不平分
B
【解析】
试题分析：先根据题意画出图形，再根据SSS证得△ABO≌△ACO，即可得到∠BAO=∠CAO，最后根据等腰三角形的三线合一的性质求解即可.
连接AO并延长
在△ABO和△ACO中，AB＝AC，OB＝OC，AO=AO
∴△ABO≌△ACO（SSS），
∴∠BAO=∠CAO，
∴AO垂直且平分BC
故选B． 已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=CG，连接BG并延长交DE于F．
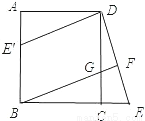
（1）求证：△BCG≌△DCE；
（2）将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形，并说明理由。
（1）答案见解析；（2）答案见解析
【解析】试题分析：（1）由正方形ABCD，得BC=CD，∠BCD=∠DCE=90°，又CG=CE，所以△BCG≌△DCE（SAS）．
（2）由（1）得BG=DE，又由旋转的性质知AE′=CE=CG，所以BE′=DG，从而证得四边形E′BGD为平行四边形．
（1）证明：∵四边形ABCD是正方形，
∴BC=CD，∠BCD=90°．
∵∠... 如图，四边形ABCD的对角线相交于点O，AO=CO，请添加一个条件_________
（只添一个即可），使四边形ABCD是平行四边形
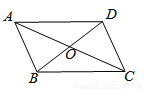
BO=DO
【解析】【解析】
∵AO=CO，BO=DO，∴四边形ABCD是平行四边形．故答案为：BO=DO． 点A、B、C是平面内不在同一条直线上的三点，点D是平面内任意一点，若A、B、C、D四点恰能构成一个平行四边形，则在平面内符合这样条件的点D有（ ）
A.1个 B.2个 C.3个 D.4个
C.
【解析】
试题分析：如图，在一个平面内，不在同一条直线上的三点，与D点恰能构成一个平行四边形，符合这样条件的点D有3个．故答案选C． 足球世界杯比赛分成8个小组,每个小组4个队,小组内进行单循环比赛(每个队都与该小组的其他队比赛一场),选出2个队进入16强.比赛规定胜一场得3分,平一场得1分,负一场得0分.请问:
(1)每个小组共比赛多少场?
(2)在小组比赛中,有一个队比赛结束后积分为6分,该队出线这一事件是什么事件?
(1)共比赛6场；(2)随机事件.
【解析】试题分析：对于（1），每个小组有4个队，每队要和其余的3个队进行比赛，故要比赛（4×3）场，而每两队之间只比赛一场，因此再除以2可完成解答；
对于（2），结合（1）的结论，先求出每组的最高得分，再求出剩下的分数，然后结合确定事件和随机事件的概念进行判断，即可完成解答.
【解析】
（1）(4×3) ÷2=6（场），
故每个小组... 计算
【解析】试题分析：先乘除，后加减，按照运算顺序进行运算即可.
原式 计算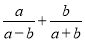
等于( )
A. 
B. 
C. 
D. 
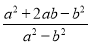
D
【解析】试题分析：原式＝
＝
＝．
故选D．