题目内容
15.一个不透明的袋子中装有两个黑球和一个白球,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球后,放回并摇匀,再随机摸出一个小球,则两次摸出的小球都是黑球的概率为$\frac{4}{9}$.分析 画树状图展示所有9种等可能的结果数,再找出两次摸出的小球都是黑球的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有9种等可能的结果数,其中两次摸出的小球都是黑球的结果数为4,
所以两次摸出的小球都是黑球的概率=$\frac{4}{9}$.
故答案为$\frac{4}{9}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.

练习册系列答案
相关题目
10. 如图,飞机飞行高度BC为1500m,飞行员看地平面指挥塔A的俯角为α,则飞机与指挥塔A的距离为( ) m.
如图,飞机飞行高度BC为1500m,飞行员看地平面指挥塔A的俯角为α,则飞机与指挥塔A的距离为( ) m.
 如图,飞机飞行高度BC为1500m,飞行员看地平面指挥塔A的俯角为α,则飞机与指挥塔A的距离为( ) m.
如图,飞机飞行高度BC为1500m,飞行员看地平面指挥塔A的俯角为α,则飞机与指挥塔A的距离为( ) m.| A. | $\frac{1500}{sinα}$ | B. | 1500sinα | C. | 1500cosα | D. | $\frac{1500}{tanα}$ |
20.一个长方形的周长为26cm,若这个长方形的长减少1cm,宽增加2cm,就可成为一个正方形,设这个长方形的长为xcm,可列方程( )
| A. | x+1=(26-x)-2 | B. | x+1=(13-x)-2 | C. | x-1=(26-x)+2 | D. | x-1=(13-x)+2 |
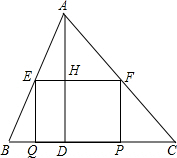 如图所示,在△ABC中,BC=10,高AD=8,矩形=EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
如图所示,在△ABC中,BC=10,高AD=8,矩形=EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H. 如图所示,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是②或③或④.
如图所示,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是②或③或④.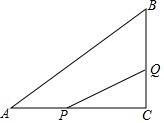 如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动
如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动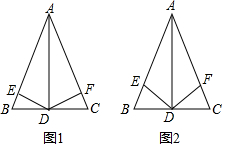 (1)如图1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于点E,DF⊥AC于点F.证明:DE=DF.
(1)如图1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于点E,DF⊥AC于点F.证明:DE=DF.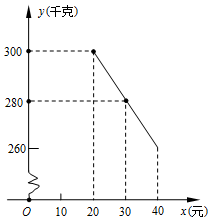 草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.