题目内容
4.在围棋盒中有x颗白色棋子和y颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是$\frac{1}{3}$,如再往盒中放进4颗黑色棋子,取得白色棋子的概率变为$\frac{1}{5}$,则x2+y2=20.分析 先根据白色棋子的概率是$\frac{1}{3}$,得到一个方程,再往盒中放进4颗黑色棋子,取得白色棋子的概率变为$\frac{1}{5}$,再得到一个方程,求解即可.
解答 解:由题意得$\left\{\begin{array}{l}{\frac{x}{x+y}=\frac{1}{3}}\\{\frac{x}{x+y+4}=\frac{1}{5}}\end{array}\right.$,
解得:x=2,y=4,
所以x2+y2=20,
故答案为:20
点评 本题主要考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$;关键是得到两个关于概率的方程.

练习册系列答案
相关题目
12.下列去括号运算中,正确的是( )
| A. | a2-(a-2b+3c)=a2-a-2b+3c | B. | a+(-x+y-2)=a-x-y-2 | ||
| C. | (2a+b)-2(a2-b2)=2a+b-2a2+b2 | D. | -(x+y)+(a-1)=-x-y+a |
19.在△ABC中,∠C=90°,下列选项中的关系式正确的是( )
| A. | sinA=$\frac{AC}{AB}$ | B. | cosB=$\frac{AC}{BC}$ | C. | tanA=$\frac{BC}{AB}$ | D. | AC=AB•cosA |
9.已知无理数x=$\sqrt{5}$+2的小数部分是y,则xy的值是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
13.已知:点A,B,C在同一条直线上,点M、N分别是AB、AC的中点,如果AB=10cm,AC=8cm,那么线段MN的长度为( )
| A. | 6cm | B. | 9cm | C. | 3cm或6cm | D. | 1cm或9cm |
14.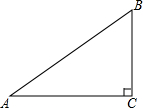 如图,Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值为( )
如图,Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值为( )
 如图,Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值为( )
如图,Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图,已知△ABC内接于⊙O,CD是⊙O的切线与半径OB的延长线交于点D,∠A=30°,求∠BCD的度数.
如图,已知△ABC内接于⊙O,CD是⊙O的切线与半径OB的延长线交于点D,∠A=30°,求∠BCD的度数.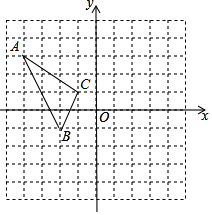 如图,在平面直角坐标系中,△ABC的顶点A(-4,3),B(-2,-1),C(-1,1)均在正方形网格的格点上,画出△ABC关于y轴对称的△A1B1C1,并写出点A的对应点A1的坐标.
如图,在平面直角坐标系中,△ABC的顶点A(-4,3),B(-2,-1),C(-1,1)均在正方形网格的格点上,画出△ABC关于y轴对称的△A1B1C1,并写出点A的对应点A1的坐标.