题目内容
7.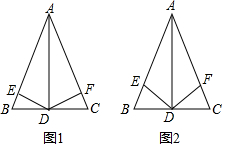 (1)如图1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于点E,DF⊥AC于点F.证明:DE=DF.
(1)如图1:在△ABC中,AB=AC,AD⊥BC,DE⊥AB于点E,DF⊥AC于点F.证明:DE=DF.(2)如图2,在△ABC中,AB=AC,AD⊥BC,DE和DF分别平分∠ADB和∠ADC,求证:DE=DF.
分析 (1)由等腰三角形的性质和角平分线的性质定理直接证明即可;
(2)利用等腰三角形的性质和全等三角形的判定定理ASA证得△AED≌△AFD,则由该全等三角形的对应边相等得到DE=DF.
解答 解:
(1)证明:∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
∵DE⊥AB,DF⊥AC
∴DE=DF;
(2)证明:∵AB=AC,AD⊥BC
∴∠BAD=∠CAD,
∵DE平分∠ADB,DF平分和∠ADC,
∴∠ADE=∠ADF=45°,
在△AED和△AFD中,
$\left\{\begin{array}{l}{∠BAD=∠CAD}\\{AD=AD}\\{∠ADE=∠ADF}\end{array}\right.$,
∴△AED≌△AFD(ASA),
∴DE=DF.
点评 本题考查了全等三角形的判定与性质和等腰三角形的性质.此题利用了等腰三角形“三线合一”的性质推知来证明三角形全等的对应角.

练习册系列答案
相关题目
12.下列去括号运算中,正确的是( )
| A. | a2-(a-2b+3c)=a2-a-2b+3c | B. | a+(-x+y-2)=a-x-y-2 | ||
| C. | (2a+b)-2(a2-b2)=2a+b-2a2+b2 | D. | -(x+y)+(a-1)=-x-y+a |
19.在△ABC中,∠C=90°,下列选项中的关系式正确的是( )
| A. | sinA=$\frac{AC}{AB}$ | B. | cosB=$\frac{AC}{BC}$ | C. | tanA=$\frac{BC}{AB}$ | D. | AC=AB•cosA |
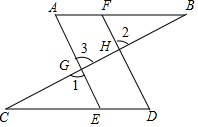 请把以下证明过程补充完整,并在下面的括号内填上推理理由:
请把以下证明过程补充完整,并在下面的括号内填上推理理由: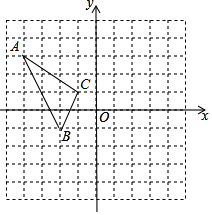 如图,在平面直角坐标系中,△ABC的顶点A(-4,3),B(-2,-1),C(-1,1)均在正方形网格的格点上,画出△ABC关于y轴对称的△A1B1C1,并写出点A的对应点A1的坐标.
如图,在平面直角坐标系中,△ABC的顶点A(-4,3),B(-2,-1),C(-1,1)均在正方形网格的格点上,画出△ABC关于y轴对称的△A1B1C1,并写出点A的对应点A1的坐标.