题目内容
3.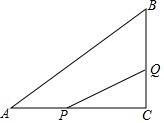 如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动
如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P沿AC边从点A以1cm/s的速度向终点C运动,同时点Q从点C以2cm/s的速度沿CB、BA边向终点A运动(1)当点Q在CB边上运动时,点P、Q出发几秒后,△PCQ的面积为12cm2;
(2)当点Q在CB边上运动时,点P、Q出发几秒后,△PCQ与△ACP相似;
(3)求整个运动过程中,△APQ的面积S与运动时间t的函数关系式.
分析 (1)设点P、Q同时出发t秒后,△PCQ的面积为12cm2,则AP=t,CQ=2t,再根据△PCQ的面积为12cm2,列出一元二次方程,求得t的值即可;
(2)根据△PCQ与△ACB相似,分两种情况讨论:当△PCQ∽△ACB时,$\frac{PC}{AC}=\frac{CQ}{CB}$;当△PCQ∽△BCA时,$\frac{PC}{BC}=\frac{CQ}{CA}$,分别根据比例式进行求解判断即可;
(3)根据整个运动过程中,点Q的位置需要分两种情况进行讨论:当点Q在BC上运动时,0≤t≤3;当点Q在BA上运动时,3<t≤8,BQ+BC=2t.分别根据三角形的面积计算方法,求得△APQ的面积S与运动时间t的函数关系式.
解答 解:(1)设点P、Q同时出发t秒后,△PCQ的面积为12cm2,则AP=t,CQ=2t,
∵AC=8,BC=6,
∴PC=8-t,CQ=2t,
∵BQ=6-2t≥0.
∴0≤t≤3,
∵△PCQ的面积为12cm2,
∴${S_{△PCQ}}=\frac{1}{2}×(8-t)×2t=12$,
∴t2-8t+12=0,
∴t=2或6(舍去),
∴点P、Q同时出发2秒后,△PCQ的面积为12cm2.
(2)∵△PCQ与△ACB相似,
∴当△PCQ∽△ACB时,$\frac{PC}{AC}=\frac{CQ}{CB}$,
即$\frac{8-t}{8}=\frac{2t}{6}$,
∴$t=\frac{24}{11}$;
当△PCQ∽△BCA时,$\frac{PC}{BC}=\frac{CQ}{CA}$,
即$\frac{8-t}{6}=\frac{2t}{8}$,
∴$t=\frac{16}{5}$>3(不合题意),
∴当P、Q同时出发$\frac{24}{11}$秒后,△PCQ与△ACB相似.
(3)如图所示,当点Q在BC上运动时,0≤t≤3,AP=t,CQ=2t,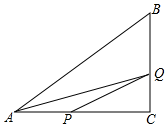
∴$S=\frac{1}{2}t×2t={t^2}$;
如图所示,当点Q在BA上运动时,3<t≤8,BQ+BC=2t.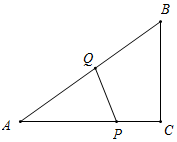
∵AC=8,BC=6,∠C=90°,
∴AB=10,
∴AQ=10+6-2t=16-2t,
∵$sinA=\frac{3}{5}$,
∴△APQ中,AP边上的高为:$\frac{3}{5}$(16-2t),
∴$S=\frac{1}{2}t(16-2t)×\frac{3}{5}=\frac{3}{5}t(8-t)=-\frac{3}{5}{t^2}+\frac{24}{5}t$.
综上所述,△APQ的面积S与运动时间t的函数关系式为:S=$\left\{\begin{array}{l}{t^2}(0≤t≤3)\\-\frac{3}{5}{t^2}+\frac{24}{5}(3<t≤8)\end{array}\right.$.
点评 本题属于相似形综合题,主要考查了相似三角形的判定与性质,三角形的面积公式的求法和一元二次方程的解的情况的综合应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程再求解.解题时注意分类思想的运用.

| A. | a2-(a-2b+3c)=a2-a-2b+3c | B. | a+(-x+y-2)=a-x-y-2 | ||
| C. | (2a+b)-2(a2-b2)=2a+b-2a2+b2 | D. | -(x+y)+(a-1)=-x-y+a |
| A. | 6cm | B. | 9cm | C. | 3cm或6cm | D. | 1cm或9cm |
 如图,已知△ABC内接于⊙O,CD是⊙O的切线与半径OB的延长线交于点D,∠A=30°,求∠BCD的度数.
如图,已知△ABC内接于⊙O,CD是⊙O的切线与半径OB的延长线交于点D,∠A=30°,求∠BCD的度数.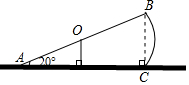 如图,跷跷板AB的一端A碰到地面时,AB与地面的夹角为20°,且
如图,跷跷板AB的一端A碰到地面时,AB与地面的夹角为20°,且