题目内容
5.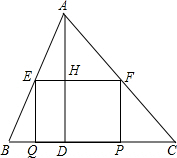 如图所示,在△ABC中,BC=10,高AD=8,矩形=EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
如图所示,在△ABC中,BC=10,高AD=8,矩形=EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.(1)求证:$\frac{AH}{AD}$=$\frac{EF}{BC}$;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求其最大值.
分析 (1)根据矩形的性质得出EQ=HD=FP,EF∥BC,推出△AEF∽△ABC,根据相似三角形的性质推出即可;
(2)根据矩形的面积公式,可以把面积表示成关于EF的长的函数,根据函数的性质即可求解.
解答 (1)证明:∵四边EFPQ是矩形,
∴EQ=HD=FP,EF∥BC,
∴△AEF∽△ABC,
∴$\frac{AH}{AD}$=$\frac{EF}{BC}$(相似三角形对应边上的高的比等于相似比).
(2)解:∵由(1)得$\frac{AH}{AD}$=$\frac{EF}{BC}$,
∵BC=10,AD=8,EF=x,
∴$\frac{AH}{8}$=$\frac{x}{10}$.
∴AH=$\frac{4}{5}$x.
∴EQ=HD=AD-AH=8-$\frac{4}{5}$x.
∴y=EF×EQ=x(8-$\frac{4}{5}$x)=-$\frac{4}{5}$x2+8x=-$\frac{4}{5}$(x-5)2+20.
∵a=-$\frac{4}{5}$<0,
∴当x=5时,y的最大值为20.
点评 本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
10.已知a-b=3,ab=2,则a2-ab+b2的值为( )
| A. | 9 | B. | 13 | C. | 11 | D. | 8 |
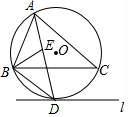 如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点D,且l∥BC.
如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点D,且l∥BC. 已知C、D是线段AB上的两点,点C是AD的中点,AB=10cm,AC=4cm,则DB的长度为2 cm.
已知C、D是线段AB上的两点,点C是AD的中点,AB=10cm,AC=4cm,则DB的长度为2 cm. 如图,已知△ABC内接于⊙O,CD是⊙O的切线与半径OB的延长线交于点D,∠A=30°,求∠BCD的度数.
如图,已知△ABC内接于⊙O,CD是⊙O的切线与半径OB的延长线交于点D,∠A=30°,求∠BCD的度数.