题目内容
19.若关于字母x的多项式-5x2-2mx2+2x-1+x2-3nx+5不含二次项和一次项,求m、n值.分析 先确定二次项及一次项的系数,再令其为0即可求m,n的值.
解答 解:-5x2-2mx2+2x-1+x2-3nx+5=(-5-2m+1)x2+(2-3n)x+4,
∵多项式-5x2-2mx2+2x-1+x2-3nx+5不含二次项和一次项,
∴-5-2m+1=0,2-3n=0,
解得m=2,n=$\frac{2}{3}$.
点评 此题考查了多项式和代数式求值,关键是先确定二次项及一次项的系数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.在△ABC中,AD是∠BAC的平分线,若∠B=50°,∠C=70°,则∠CAD的度数是( )
| A. | 15° | B. | 30° | C. | 60° | D. | 120° |
7.若点A(-1,y1),B(1,y2),C(2,y3)都在反比例函数y=$\frac{3}{x}$的图象上,则y1,y2,y3的大小关系为( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y3<y2<y1 |
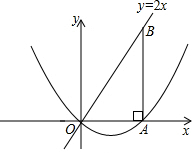 如图,在平面直角坐标系中,点B在直线y=2x上,过点B作x轴的垂线,垂足为A,OA=5,若抛物线y=x2+bx+c过O、A两点.
如图,在平面直角坐标系中,点B在直线y=2x上,过点B作x轴的垂线,垂足为A,OA=5,若抛物线y=x2+bx+c过O、A两点.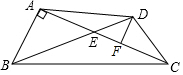 如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,DF∥AB,交AC于F,∠DCE=30°,AB=DC=5,BC=13,求AC的长和四边形ABCD的面积.
如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,DF∥AB,交AC于F,∠DCE=30°,AB=DC=5,BC=13,求AC的长和四边形ABCD的面积.