题目内容
7．若点A（-1，y1），B（1，y2），C（2，y3）都在反比例函数y=$\frac{3}{x}$的图象上，则y1，y2，y3的大小关系为（ ）| A． | y1＜y2＜y3 | B． | y1＜y3＜y2 | C． | y3＜y1＜y2 | D． | y3＜y2＜y1 |
分析 根据反比例函数的增减性可得．
解答 解：∵反比例函数y=$\frac{3}{x}$中，当x＞0时，y随x的增大而减小，
∴y3＜y2，
∵y1＜0，
∴y1＜y3＜y2，
故选：B．
点评 本题主要考查反比例函数图象上点的坐标特征，熟练掌握反比例函数的增减性是解题的关键．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知：有理数a、b、c在数轴上如图所示．化简：|a|+3|c-a|+|b+c|．
2．
如图．已知Rt△ABC中，∠B=90°，∠A=30°，AB=2$\sqrt{3}$，将△ABC绕顶点C顺时针旋转至△A′B′C′位置且A，C，B′共线，则A经过的路线长为（ ）
如图．已知Rt△ABC中，∠B=90°，∠A=30°，AB=2$\sqrt{3}$，将△ABC绕顶点C顺时针旋转至△A′B′C′位置且A，C，B′共线，则A经过的路线长为（ ）| A． | 8 | B． | 4$\sqrt{3}$ | C． | $\frac{32}{3}$π | D． | $\frac{8}{3}$π |
16．若式子$\sqrt{3-x}$有意义，在实数范围内有意义，则x的取值范围是（ ）
| A． | x≥3 | B． | x≤3 | C． | x＞3 | D． | x＜3 |
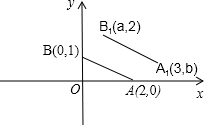如图，点A，B的坐标分别为（2，0），（0，1），若将线段AB平移至点A1B1，那么a-b=0．