题目内容
6.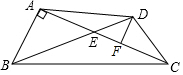 如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,DF∥AB,交AC于F,∠DCE=30°,AB=DC=5,BC=13,求AC的长和四边形ABCD的面积.
如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC=90°,DF∥AB,交AC于F,∠DCE=30°,AB=DC=5,BC=13,求AC的长和四边形ABCD的面积.
分析 先在Rt△ABC中,利用勾股定理求出AC,再在Rt△DFC中,用含30°的直角三角形的性质求出DF,最后用面积的和即可求出结论.
解答 解:在Rt△ABC中,AB=5,BC=13,
根据勾股定理得,AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=12,
∵DF∥AB,
∴∠AFD=∠BAC=90°,
∴∠DFC=90°,
在Rt△DFC中,∠DCE=30°,DC=5,
∴DF=$\frac{1}{2}$CD=$\frac{5}{2}$,
∴S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}$AC•AB+$\frac{1}{2}$AC•DF=$\frac{1}{2}$×12×5+$\frac{1}{2}$×12×$\frac{5}{2}$=45.
即:AC的长为12,四边形ABCD的面积为45.
点评 此题主要考查了勾股定理,含30°的直角三角形的性质,平行线的性质,不规则图形的面积的计算方法,三角形的面积公式,解本题的关键是求出AC和DF.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
18.在平面直角坐标系中,点P(3,4)到原点的距离是( )
| A. | 3 | B. | 4 | C. | 5 | D. | ±5 |
16.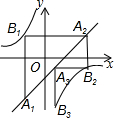 如图,已知:n为正整数,点A1(x1,y1),A2(x2,y2),A3(x3,y3),A4(x4,y4)…An(xn,yn)均在直线y=x-1上,点B1(m1,p1),B2(m2,p2),B3(m3,p3)…Bn(mn,pn)均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,A3B3⊥x轴,…,AnBn⊥x轴,BnAn+1⊥y轴,若点A1的横坐标为-1,则点A2017的坐标为( )
如图,已知:n为正整数,点A1(x1,y1),A2(x2,y2),A3(x3,y3),A4(x4,y4)…An(xn,yn)均在直线y=x-1上,点B1(m1,p1),B2(m2,p2),B3(m3,p3)…Bn(mn,pn)均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,A3B3⊥x轴,…,AnBn⊥x轴,BnAn+1⊥y轴,若点A1的横坐标为-1,则点A2017的坐标为( )
 如图,已知:n为正整数,点A1(x1,y1),A2(x2,y2),A3(x3,y3),A4(x4,y4)…An(xn,yn)均在直线y=x-1上,点B1(m1,p1),B2(m2,p2),B3(m3,p3)…Bn(mn,pn)均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,A3B3⊥x轴,…,AnBn⊥x轴,BnAn+1⊥y轴,若点A1的横坐标为-1,则点A2017的坐标为( )
如图,已知:n为正整数,点A1(x1,y1),A2(x2,y2),A3(x3,y3),A4(x4,y4)…An(xn,yn)均在直线y=x-1上,点B1(m1,p1),B2(m2,p2),B3(m3,p3)…Bn(mn,pn)均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,A3B3⊥x轴,…,AnBn⊥x轴,BnAn+1⊥y轴,若点A1的横坐标为-1,则点A2017的坐标为( )| A. | (-1,-2) | B. | (2,1) | C. | ($\frac{1}{2}$,$-\frac{1}{2}$) | D. | ($\frac{1}{2}$,-2) |
16.若式子$\sqrt{3-x}$有意义,在实数范围内有意义,则x的取值范围是( )
| A. | x≥3 | B. | x≤3 | C. | x>3 | D. | x<3 |
 已知:有理数a、b、c在数轴上如图所示.化简:|a|+3|c-a|+|b+c|.
已知:有理数a、b、c在数轴上如图所示.化简:|a|+3|c-a|+|b+c|.