题目内容
9.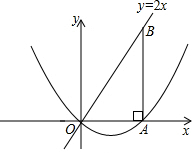 如图,在平面直角坐标系中,点B在直线y=2x上,过点B作x轴的垂线,垂足为A,OA=5,若抛物线y=x2+bx+c过O、A两点.
如图,在平面直角坐标系中,点B在直线y=2x上,过点B作x轴的垂线,垂足为A,OA=5,若抛物线y=x2+bx+c过O、A两点.(1)求该抛物线的解析式;
(2)若点B关于y轴对称的对称点为C,判断点C是否在该抛物线上,并说明理由.
分析 (1)利用代入法可得二次函数的解析式;
(2)由OA=5,BA⊥x轴,可得B点横坐标为5,将x=5代入y=2x可得y=10,即可得B点的坐标,易得C点坐标为(-5,10),将x=-5代入(1)所得解析式即可判断.
解答 解:(1)∵OA=5,
∴A(5,0),
抛物线y=x2+bx+c过O、A两点,
∴将O、A两点代入抛物线y=x2+bx+c得,
∴$\left\{\begin{array}{l}{0=c}\\{\;}\\{0{=5}^{2}+5b}\end{array}\right.$
解得$\left\{\begin{array}{l}{b=-5}\\{\;}\\{c=0}\end{array}\right.$,
∴抛物线的解析式为:y=x2-5x;
(2)点C不在该抛物线上.
∵OA=5,BA⊥x轴,
∴B点横坐标为5,
将x=5代入y=2x可得y=10
∴B点的坐标为(5,10),
∵点B关于y轴对称的对称点为C,
∴C点坐标为(-5,10),
当x=-5时,y=x2-5x=25+25=50≠10,
∴点C不在该抛物线上.
点评 本题主要考查了待定系数法求二次函数的解析式,利用代入法是解答此题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
17.化简2$\sqrt{2}$-$\frac{3}{\sqrt{2}}$+$\frac{16}{\sqrt{8}}$的结果是( )
| A. | $\frac{9}{2}$$\sqrt{2}$ | B. | -$\frac{7}{2}$$\sqrt{2}$ | C. | $\frac{9}{\sqrt{2}}$ | D. | -$\frac{7}{\sqrt{2}}$ |
18.在平面直角坐标系中,点P(3,4)到原点的距离是( )
| A. | 3 | B. | 4 | C. | 5 | D. | ±5 |

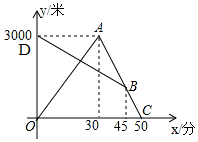 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题: