题目内容
7．两条直线相交，如果其中一组对顶角之和是220°，则这两条直线相交所得到的四个角的度数分别是110°，70°，110°，70°．分析 根据对顶角的性质，可得一个角，根据邻补角，可得到答案．
解答 解：设对顶角中的一个是x°，
由对顶角的性质，得
2x=110°，
解得x=110°，
由邻补角的性质，得
180°-110°=70°，
故答案为：110°，70°，110°，70°．
点评 本题考查了对顶角、邻补角，利用对顶角的性质，邻补角的性质是解题关键．
练习册系列答案
相关题目
17．化简2$\sqrt{2}$-$\frac{3}{\sqrt{2}}$+$\frac{16}{\sqrt{8}}$的结果是（ ）
| A． | $\frac{9}{2}$$\sqrt{2}$ | B． | -$\frac{7}{2}$$\sqrt{2}$ | C． | $\frac{9}{\sqrt{2}}$ | D． | -$\frac{7}{\sqrt{2}}$ |
18．在平面直角坐标系中，点P（3，4）到原点的距离是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | ±5 |
2．若a＞b，则下列不等式中成立的是（ ）
| A． | a-5＞b-5 | B． | $\frac{a}{5}$＜$\frac{b}{5}$ | C． | a+5＞b+6 | D． | -a＞-b |
16．
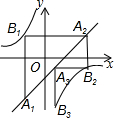如图，已知：n为正整数，点A1（x1，y1），A2（x2，y2），A3（x3，y3），A4（x4，y4）…An（xn，yn）均在直线y=x-1上，点B1（m1，p1），B2（m2，p2），B3（m3，p3）…Bn（mn，pn）均在双曲线y=-$\frac{1}{x}$上，并且满足：A1B1⊥x轴，B1A2⊥y轴，A2B2⊥x轴，B2A3⊥y轴，A3B3⊥x轴，…，AnBn⊥x轴，BnAn+1⊥y轴，若点A1的横坐标为-1，则点A2017的坐标为（ ）
如图，已知：n为正整数，点A1（x1，y1），A2（x2，y2），A3（x3，y3），A4（x4，y4）…An（xn，yn）均在直线y=x-1上，点B1（m1，p1），B2（m2，p2），B3（m3，p3）…Bn（mn，pn）均在双曲线y=-$\frac{1}{x}$上，并且满足：A1B1⊥x轴，B1A2⊥y轴，A2B2⊥x轴，B2A3⊥y轴，A3B3⊥x轴，…，AnBn⊥x轴，BnAn+1⊥y轴，若点A1的横坐标为-1，则点A2017的坐标为（ ）| A． | （-1，-2） | B． | （2，1） | C． | （$\frac{1}{2}$，$-\frac{1}{2}$） | D． | （$\frac{1}{2}$，-2） |
已知：有理数a、b、c在数轴上如图所示．化简：|a|+3|c-a|+|b+c|．