题目内容
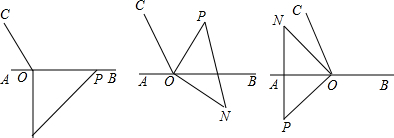
如图1,点O为直线AB上一点,∠AOC=60°,将一直角三角板的直角顶点放在点O处,一边OP在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O旋转至图2,使一边OP恰好平分∠BOC,求∠BOP的度数;
(2)将图1中的三角板绕点O按每秒10°的速度沿顺时针方向旋转一周,若t秒后∠CON=90°,则t的值为 秒.(直接写出结果);
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOP与∠NOC之间的数量关系,并说明理由.
(1)将图1中的三角板绕点O旋转至图2,使一边OP恰好平分∠BOC,求∠BOP的度数;
(2)将图1中的三角板绕点O按每秒10°的速度沿顺时针方向旋转一周,若t秒后∠CON=90°,则t的值为
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOP与∠NOC之间的数量关系,并说明理由.

考点:角的计算,角平分线的定义
专题:
分析:(1)由角的平分线的定义和等角的余角相等求解;
(2)由∠AOC=60°,∠CON=90°,可得顺时针旋转60°或240°时满足题意,据此求出t=6或24;
(3)因为∠PON=90°,∠AOC=60°,所以∠AOP=90°-∠AON、∠NOC=60°-∠AON,然后求差即可.
(2)由∠AOC=60°,∠CON=90°,可得顺时针旋转60°或240°时满足题意,据此求出t=6或24;
(3)因为∠PON=90°,∠AOC=60°,所以∠AOP=90°-∠AON、∠NOC=60°-∠AON,然后求差即可.
解答:解:∵∠AOC=60°,
∴∠BOC=120°,
又∵OP平分∠BOC,
∴∠BOP=
∠BOC=60°,
(2)有两种情形:①如图4所示:作OM⊥AB,
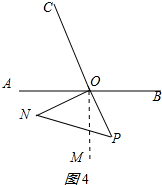
∵∠CON=90°,∠AOC=60°,
∴∠AON=30°,∴∠MON=60°,∴t=60°÷10°=6;
②如图5所示:作OM⊥AB,
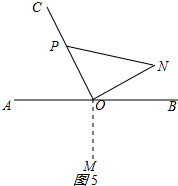
∵∠CON=90°,∠AOC=60°,
∴∠NOB=30°,∴∠NOM=120°,
∴(360°-120°)÷10°=24;
因此t=6或24秒
(3)∠AOP-∠NOC=30°.理由如下:
∵∠PON=90°,∠AOC=60°,
∴∠AOP=90°-∠AON,∠NOC=60°-∠AON,
∴∠AOP-∠NOC=(90°-∠AON)-(60°-∠AON)=30°,
则∠AOP与∠NOC之间的数量关系是:∠AOP-∠NOC=30°.
∴∠BOC=120°,
又∵OP平分∠BOC,
∴∠BOP=
| 1 |
| 2 |
(2)有两种情形:①如图4所示:作OM⊥AB,

∵∠CON=90°,∠AOC=60°,
∴∠AON=30°,∴∠MON=60°,∴t=60°÷10°=6;
②如图5所示:作OM⊥AB,

∵∠CON=90°,∠AOC=60°,
∴∠NOB=30°,∴∠NOM=120°,
∴(360°-120°)÷10°=24;
因此t=6或24秒
(3)∠AOP-∠NOC=30°.理由如下:
∵∠PON=90°,∠AOC=60°,
∴∠AOP=90°-∠AON,∠NOC=60°-∠AON,
∴∠AOP-∠NOC=(90°-∠AON)-(60°-∠AON)=30°,
则∠AOP与∠NOC之间的数量关系是:∠AOP-∠NOC=30°.
点评:此题考查了角的计算,关键是应该认真审题并仔细观察图形,找出各个量之间的关系,是解决问题的关键.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
计算(2+1)(22+1)(24+1)…(232+1)的结果为( )
| A、235+2 |
| B、264+1 |
| C、264-1 |
| D、232-1 |
 如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为( )
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则tan∠EFO的值为( )| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
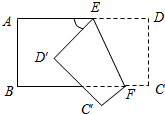 如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠EFB等于( )
如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠EFB等于( )| A、50° | B、55° |
| C、60° | D、65° |
 如图,点C为线段AB上一点,若线段AC=12cm,AC:CB=3:2,D、E两点分别为AC、AB的中点,求DE的长.
如图,点C为线段AB上一点,若线段AC=12cm,AC:CB=3:2,D、E两点分别为AC、AB的中点,求DE的长. 如图,P是定长线段AB上一点,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB先向左运动(C在线段AP上,D在线段BP上).
如图,P是定长线段AB上一点,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB先向左运动(C在线段AP上,D在线段BP上).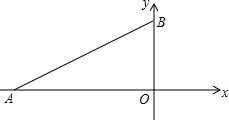 如图,在平面直角坐标系中,点A(-6,0),点B(0,2
如图,在平面直角坐标系中,点A(-6,0),点B(0,2 如图,直线AB、CD相交于O,且∠AOC:∠BOC=1:2,∠AOF=∠BOF=90°,OE平分∠BOC,求:∠EOF的度数.
如图,直线AB、CD相交于O,且∠AOC:∠BOC=1:2,∠AOF=∠BOF=90°,OE平分∠BOC,求:∠EOF的度数.