题目内容
 如图,P是定长线段AB上一点,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB先向左运动(C在线段AP上,D在线段BP上).
如图,P是定长线段AB上一点,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB先向左运动(C在线段AP上,D在线段BP上).(1)若C、D运动到任一时刻时,总有PD=2AC,请说明AP=
| 1 |
| 3 |
(2)在(1)的条件下,Q是直线AB上一点,且AQ-BQ=PQ,求
| PQ |
| AB |
(3)在(1)的条件下,若C、D运动5秒后,恰好有CD=
| 1 |
| 2 |
| MN |
| AB |
考点:一元一次方程的应用,两点间的距离
专题:
分析:(1)设C、D运动时间是t秒,由已知条件PD=2AC求得PB=2AP,依此即可求解;
(2)由题设画出图示,根据AQ-BQ=PQ求得AQ=PQ+BQ;然后求得AP=BQ,从而求得PQ与AB的关系;
(3)当点C停止运动时,有CD=
AB,从而求得CM与AB的数量关系;然后求得以AB表示的PM与PN的值,所以MN=PN-PM=
AB.
(2)由题设画出图示,根据AQ-BQ=PQ求得AQ=PQ+BQ;然后求得AP=BQ,从而求得PQ与AB的关系;
(3)当点C停止运动时,有CD=
| 1 |
| 2 |
| 1 |
| 12 |
解答:解:(1)设C、D运动时间是t秒,
∵PD=2AC,PB-BD=2(AP-PC),即PB-2t=2(AP-t),
∴PB=2AP,
∴
=2,
∴AP=
AB;
(2)如图:

∵AQ-BQ=PQ,
∴AQ=PQ+BQ;
又∵AQ=AP+PQ,
∴AP=BQ,
∴PQ=
AB,
∴
=
.
当点Q'在AB的延长线上时
AQ'-AP=PQ'
所以AQ'-BQ'=PQ=AB
所以
=1;
(3)②
的值不变.
理由:如图,当点C停止运动时,有CD=
AB,
∴CM=
AB;
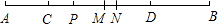
∴PM=CM-CP=
AB-5,
∵PD=PB-BD=
AB-10,
∴PN=
(
AB-10)=
AB-5,
∴MN=PN-PM=
AB;
当点C停止运动,D点继续运动时,MN的值不变,所以MN=
=
.
∵PD=2AC,PB-BD=2(AP-PC),即PB-2t=2(AP-t),
∴PB=2AP,
∴
| PB |
| AP |
∴AP=
| 1 |
| 3 |
(2)如图:

∵AQ-BQ=PQ,
∴AQ=PQ+BQ;
又∵AQ=AP+PQ,
∴AP=BQ,
∴PQ=
| 1 |
| 3 |
∴
| PQ |
| AB |
| 1 |
| 3 |
当点Q'在AB的延长线上时
AQ'-AP=PQ'
所以AQ'-BQ'=PQ=AB
所以
| PQ |
| AB |
(3)②
| MN |
| AB |
理由:如图,当点C停止运动时,有CD=
| 1 |
| 2 |
∴CM=
| 1 |
| 4 |
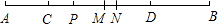
∴PM=CM-CP=
| 1 |
| 4 |
∵PD=PB-BD=
| 2 |
| 3 |
∴PN=
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
∴MN=PN-PM=
| 1 |
| 12 |
当点C停止运动,D点继续运动时,MN的值不变,所以MN=
| ||
| AB |
| 1 |
| 12 |
点评:本题考查了一元一次方程的应用,比较线段的长短.利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
下列计算错误的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知二次函数y=ax2+bx+c的x、y的部分对应值如表:则该二次函数图象的对称轴为( )
| x | -1 | 0 | 1 | 2 | 3 |
| y | 5 | 1 | -1 | -1 | 1 |
| A、y轴 | ||
B、直线x=
| ||
| C、直线x=2 | ||
| D、直线x=2 |
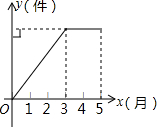 烈山留园存村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )
烈山留园存村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )| A、1月至3月每月生产总量逐月增加,4,5两月停止生产 |
| B、1月至3月每月生产总量不变,4,5两月均停止生产 |
| C、1月至3月每月生产总量逐月增加,4,5两月每月生产总量逐月减少 |
| D、1月至3月每月生产总量逐月增加,4,5两月生产量与3月持平 |
 如图,BD是∠ABC的平分线,DE∥BC交AB于点E,若∠BDE=25°,则∠ABD的度数为( )
如图,BD是∠ABC的平分线,DE∥BC交AB于点E,若∠BDE=25°,则∠ABD的度数为( )| A、50° | B、25° |
| C、15° | D、12.5° |
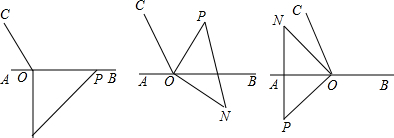
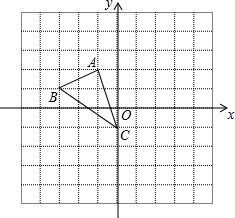 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1),
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1),