题目内容
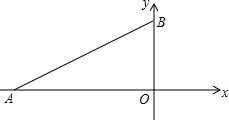 如图,在平面直角坐标系中,点A(-6,0),点B(0,2
如图,在平面直角坐标系中,点A(-6,0),点B(0,2| 3 |
考点:相似三角形的判定,坐标与图形性质
专题:计算题
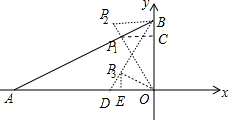
分析:由三角函数可求出∠A=30°,∠ABO=60°,作OP1⊥AB于P1,作P1C⊥y轴,过点B作BP2⊥y轴交OP1于P2,作∠ABO的平分线BD,过点O作OP3⊥BD于P3,过P3作P3E⊥x轴于E,如图,根据有两组角对应相等的两个三角形相似可判断△BP1O∽△BOA,△P2OB∽△BAO,△P3OB∽△OBA,然后分别确定P1、P2、P3的坐标.
解答:解:∵点A(-6,0),点B(0,2
),
∴OA=6,OB=2
,
∴tanA=
=
=
,
∴∠A=30°,
∴∠ABO=60°,
作OP1⊥AB于P1,作P1C⊥y轴,过点B作BP2⊥y轴交OP1于P2,作∠ABO的平分线BD,过点O作OP3⊥BD于P3,过P3作P3E⊥x轴于E,如图,
∵∠BP1O=∠BOA=90°,∠P1BO=∠OBA,
∴△BP1O∽△BOA,
在Rt△OBP1中,∵sin∠OBP1=
,
∴OP1=2
sin60°=3,
在Rt△OP1C中,∵∠P1OC=30°,
∴P1C=
OP1=
,OC=
P1C=
,
∴P1点的坐标为(-
,
);
∵∠P2OB=∠A=30°,
∴△P2OB∽△BAO,
在Rt△OP2B中,∵∠P2OB=30°,
∴P2B=
OB=
×2
=2,
∴P2点的坐标为(-2,2
);
∵∠P3BO=∠A=30°,
∴△P3OB∽△OBA,
在Rt△OP3B中,∵∠P3BO=30°,
∴OP3=
OB=
,∠P3OB=60°,
∴∠P3OE=30°,
在Rt△P3OE中,P3E=
OP3=
,OE=
P3E=
,
∴P3点的坐标为(-
,
);
综上所述,满足条件的P点坐标为(-
,
)或(-2,2
)或(-
,
).
故答案为(-
,
)或(-2,2
)或(-
,
).
| 3 |

∴OA=6,OB=2
| 3 |
∴tanA=
| OB |
| OA |
2
| ||
| 6 |
| ||
| 3 |
∴∠A=30°,
∴∠ABO=60°,
作OP1⊥AB于P1,作P1C⊥y轴,过点B作BP2⊥y轴交OP1于P2,作∠ABO的平分线BD,过点O作OP3⊥BD于P3,过P3作P3E⊥x轴于E,如图,
∵∠BP1O=∠BOA=90°,∠P1BO=∠OBA,
∴△BP1O∽△BOA,
在Rt△OBP1中,∵sin∠OBP1=
| OP1 |
| OB |
∴OP1=2
| 3 |
在Rt△OP1C中,∵∠P1OC=30°,
∴P1C=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
3
| ||
| 2 |
∴P1点的坐标为(-
| 3 |
| 2 |
3
| ||
| 2 |
∵∠P2OB=∠A=30°,
∴△P2OB∽△BAO,
在Rt△OP2B中,∵∠P2OB=30°,
∴P2B=
| ||
| 3 |
| ||
| 3 |
| 3 |
∴P2点的坐标为(-2,2
| 3 |
∵∠P3BO=∠A=30°,
∴△P3OB∽△OBA,
在Rt△OP3B中,∵∠P3BO=30°,
∴OP3=
| 1 |
| 2 |
| 3 |
∴∠P3OE=30°,
在Rt△P3OE中,P3E=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
∴P3点的坐标为(-
| 3 |
| 2 |
| ||
| 2 |
综上所述,满足条件的P点坐标为(-
| 3 |
| 2 |
3
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
故答案为(-
| 3 |
| 2 |
3
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
点评:本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了坐标与图形性质、含30度的直角三角形三边的关系.根据题意画出几何图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

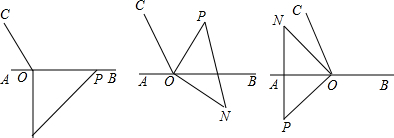
 如图,在平面内有A、B、C三点.
如图,在平面内有A、B、C三点.
 △ABC中,D是BC上一点,若
△ABC中,D是BC上一点,若