题目内容
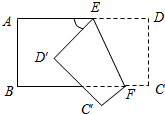 如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠EFB等于( )
如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠EFB等于( )| A、50° | B、55° |
| C、60° | D、65° |
考点:平行线的性质,翻折变换(折叠问题)
专题:
分析:由折叠的性质可得∠DEF=∠D′EF,因为∠AED′=50°,结合平角可求得∠DEF=∠D′EF=65°,平行可求得∠EFB=∠DEF=65°.
解答:解:∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DEF=∠EFB,
又由折叠的性质可得∠D′EF=∠DEF,
∵∠AED′+∠D′EF+∠DEF=180°,∠AED′=50°,
∠D′EF=∠DEF=
=65°,
∴∠EFB=∠DEF=65°.
故选D.
∴AD∥BC,
∴∠DEF=∠EFB,
又由折叠的性质可得∠D′EF=∠DEF,
∵∠AED′+∠D′EF+∠DEF=180°,∠AED′=50°,
∠D′EF=∠DEF=
| 180°-50° |
| 2 |
∴∠EFB=∠DEF=65°.
故选D.
点评:本题主要考查平行线的性质及折叠的性质,掌握两直线平行内错角相等是解题的关键.

练习册系列答案
相关题目
 如图,BD是∠ABC的平分线,DE∥BC交AB于点E,若∠BDE=25°,则∠ABD的度数为( )
如图,BD是∠ABC的平分线,DE∥BC交AB于点E,若∠BDE=25°,则∠ABD的度数为( )| A、50° | B、25° |
| C、15° | D、12.5° |
 如图,由6个相同的小正方体搭成的立体图形,若由图①变到图②,不改变的是( )
如图,由6个相同的小正方体搭成的立体图形,若由图①变到图②,不改变的是( )| A、主视图 | B、左视图 |
| C、俯视图 | D、左视图和俯视图 |
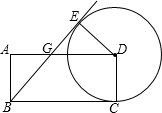 如图,矩形ABCD中,AB=1,BC=3,以D为圆心,CD为半径作⊙D,直线BE切⊙D于点E,BE交AD于点G,则AG=
如图,矩形ABCD中,AB=1,BC=3,以D为圆心,CD为半径作⊙D,直线BE切⊙D于点E,BE交AD于点G,则AG= △ABC中,D是BC上一点,若
△ABC中,D是BC上一点,若 如图,PA、PB、CD是⊙O的切线,切点分别为点A、B、E,若△PCD的周长为18cm,∠APB=60°,求⊙O的半径.
如图,PA、PB、CD是⊙O的切线,切点分别为点A、B、E,若△PCD的周长为18cm,∠APB=60°,求⊙O的半径.