题目内容
17.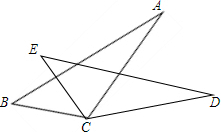 如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )| A. | AB=DE | B. | ∠B=∠E | C. | AC=DC | D. | ∠A=∠D |
分析 先求出∠ACB=∠DCE,再根据全等三角形的判定定理(SAS,ASA,AAS,SSS)逐个判断即可.
解答 解:∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
∴∠ACB=∠DCE,
A、根据BC=CE,AB=DE,∠ACB=∠DCE不能推出△ABC≌△DEC,故本选项正确;
B、因为∠ACB=∠DCE,∠B=∠E,BC=CE,所以符合ASA定理,即能推出△ABC≌△DEC,故本选项错误;
C、因为BC=CE,∠ACB=∠DCE,AC=CD,所以符合SAS定理,即能推出△ABC≌△DEC,故本选项错误;
D、因为∠A=∠D,∠ACB=∠DCE,BC=CE,所以符合AAS定理,即能推出△ABC≌△DEC,故本选项错误;
故选A.
点评 本题考查了全等三角形的判定定理的应用,能理解和运用全等三角形的判定定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,难度适中.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
6.已知(-1,y1),(-2,y2),(-4,y3)是抛物线y=-2(x+2)2+m上的点,则( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y2>y1>y3 | D. | y2>y3>y1 |
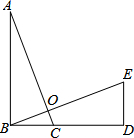 如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE=95°.
如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE=95°. 如图,四边形ABCD中,AC与BD交于点O,若BD=3DO,当OC:OA的值为$\frac{1}{2}$时,则有AB∥DC.
如图,四边形ABCD中,AC与BD交于点O,若BD=3DO,当OC:OA的值为$\frac{1}{2}$时,则有AB∥DC. 如图,四边形ABCD内接于⊙O,若四边形ABCD的外角∠DCE=65°,则∠BAD的度数是65°.
如图,四边形ABCD内接于⊙O,若四边形ABCD的外角∠DCE=65°,则∠BAD的度数是65°. 如图,在△ABC中,BC的垂直平分线分别交AB、BC于D、E,若△ACD的周长为10cm,AC=3cm,则AB=7 cm.
如图,在△ABC中,BC的垂直平分线分别交AB、BC于D、E,若△ACD的周长为10cm,AC=3cm,则AB=7 cm.