题目内容
8.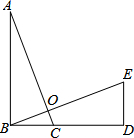 如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE=95°.
如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE=95°.
分析 根据全等得出∠A=∠EBD,∠ABC=∠BDE,求出∠BDE=∠ABC=∠ABO+∠EBD=∠ABO+∠A,即可求出答案.
解答 解:∵△ABC≌△BDE,
∴∠A=∠EBD,∠ABC=∠BDE,
∵∠AOE=95°,
∴∠BDE=∠ABC=∠ABO+∠EBD
=∠ABO+∠A
=180°-∠AOB
=180°-(180°-95°)
=95°,
故答案为:95.
点评 本题考查了三角形内角和定理,全等三角形的性质的应用,能根据全等得出∠A=∠EBD和∠ABC=∠BDE是解此题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
11.设a,b,c分别是△ABC的边长,若∠B=2∠A,则下列关系是成立的是( )
| A. | $\frac{a}{b}$$>\frac{a+b}{a+b+c}$ | B. | $\frac{a}{b}$$<\frac{a+b}{a+b+c}$ | C. | $\frac{a}{b}$=$\frac{a+b}{a+b+c}$ | D. | 无法确定 |
17.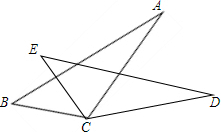 如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
 如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )| A. | AB=DE | B. | ∠B=∠E | C. | AC=DC | D. | ∠A=∠D |
18.在Rt△ABC中,∠C=90°,AC=3,BC=4,则点C到AB的距离是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{3}{4}$ |
 一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进、出水管.在打开进水管到关停进、出水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示
一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进、出水管.在打开进水管到关停进、出水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示



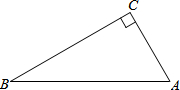 如图,在△ABC中,∠C=90°,∠A>∠B.
如图,在△ABC中,∠C=90°,∠A>∠B.