题目内容
20.若x+y+y2-4y+4=2$\sqrt{xy}$,求$\sqrt{x+y}$的值.分析 利用配方法把原式化为平方和的形式,根据非负数的性质分别求出x、y的值,根据算术平方根的概念计算即可.
解答 解:∵x+y+y2-4y+4=2$\sqrt{xy}$,
∴x-2$\sqrt{xy}$+y+y2-4y+4=0,
∴($\sqrt{x}$-$\sqrt{y}$)2+(y-2)2=0,
∴$\sqrt{x}$-$\sqrt{y}$=0,y-2=0,
解得x=2,y=2,
则$\sqrt{x+y}$=2.
点评 本题考查的是配方法的应用和非负数的性质,掌握利用配方法把原式化为平方和的形式是解题的关键,注意几个数或式的偶次方相加和为0时,则其中的每一项都必须等于0.

练习册系列答案
相关题目
11.设a,b,c分别是△ABC的边长,若∠B=2∠A,则下列关系是成立的是( )
| A. | $\frac{a}{b}$$>\frac{a+b}{a+b+c}$ | B. | $\frac{a}{b}$$<\frac{a+b}{a+b+c}$ | C. | $\frac{a}{b}$=$\frac{a+b}{a+b+c}$ | D. | 无法确定 |
17.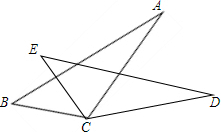 如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
 如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )| A. | AB=DE | B. | ∠B=∠E | C. | AC=DC | D. | ∠A=∠D |
 一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进、出水管.在打开进水管到关停进、出水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示
一个装有进水管和出水管的容器,从某时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进、出水管.在打开进水管到关停进、出水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示