题目内容
6．已知（-1，y1），（-2，y2），（-4，y3）是抛物线y=-2（x+2）2+m上的点，则（ ）| A． | y1＜y2＜y3 | B． | y3＜y2＜y1 | C． | y2＞y1＞y3 | D． | y2＞y3＞y1 |
分析 求出抛物线的对称轴为直线x=-2，然后根据二次函数的增减性和对称性解答即可．
解答 解：抛物线的对称轴为直线x=-2，
∵a=-2＜0，
∴x=-2时，函数值最大，
又∵-1到-2的距离比-4到-2的距离小，
∴y2＞y1＞y3．
故选C．
点评 本题考查了二次函数图象上点的坐标特征，主要利用了二次函数的增减性和对称性，求出对称轴是解题的关键．
练习册系列答案
相关题目
17．
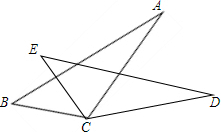如图，若BC=EC，∠BCE=∠ACD，则添加不能使△ABC≌△DBC的条件是（ ）
如图，若BC=EC，∠BCE=∠ACD，则添加不能使△ABC≌△DBC的条件是（ ）| A． | AB=DE | B． | ∠B=∠E | C． | AC=DC | D． | ∠A=∠D |
1．
如图，在△ABC中，AD⊥BC垂足为点D，AD是BC边上的中线，BE⊥AC，垂足为点E．则以下4个结论：①AB=AC；②∠EBC=$\frac{1}{2}∠BAC$；③AE=CE；④∠EBC=$\frac{1}{2}∠ABC$中正确的有（ ）
如图，在△ABC中，AD⊥BC垂足为点D，AD是BC边上的中线，BE⊥AC，垂足为点E．则以下4个结论：①AB=AC；②∠EBC=$\frac{1}{2}∠BAC$；③AE=CE；④∠EBC=$\frac{1}{2}∠ABC$中正确的有（ ）| A． | ①② | B． | ②③ | C． | ①②③ | D． | ①②③④ |
11．下列图形中，是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
18．在Rt△ABC中，∠C=90°，AC=3，BC=4，则点C到AB的距离是（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{12}{5}$ | D． | $\frac{3}{4}$ |
如图，AB=AC，∠A=36°，BD是∠ABC的角平分线，求证：△ABC∽△BCD．