题目内容
5. 如图,四边形ABCD中,AC与BD交于点O,若BD=3DO,当OC:OA的值为$\frac{1}{2}$时,则有AB∥DC.
如图,四边形ABCD中,AC与BD交于点O,若BD=3DO,当OC:OA的值为$\frac{1}{2}$时,则有AB∥DC.
分析 由BD=3DO,得$\frac{OD}{OB}=\frac{1}{2}$,于是得到$\frac{OD}{OB}=\frac{OC}{OA}$,又∠COD=∠AOB,根据相似三角形的判定推出△COD∽△AOB,由相似三角形的性质得到DCA=∠BAC,即可证得结论.
解答 当OC:OA的值为$\frac{1}{2}$时,则有AB∥DC,
证明:∵BD=3DO,
∴BO=2D0,
∴$\frac{OD}{OB}=\frac{1}{2}$,
∵$\frac{OC}{OA}=\frac{1}{2}$,
∴$\frac{OD}{OB}=\frac{OC}{OA}$,
∵∠COD=∠AOB,
∴△COD∽△AOB,
∴∠DCA=∠BAC,
AB∥DC,
故答案为$\frac{1}{2}$.
点评 本题主要考查了相似三角形的判定和性质,平行线的判定,熟练掌握相似三角形的判定和性质是解决问题的关键.

练习册系列答案
相关题目
10. 如图是二次函数y=ax2+bx+c的部分图象,由图象可知该二次函数的对称轴是( )
如图是二次函数y=ax2+bx+c的部分图象,由图象可知该二次函数的对称轴是( )
 如图是二次函数y=ax2+bx+c的部分图象,由图象可知该二次函数的对称轴是( )
如图是二次函数y=ax2+bx+c的部分图象,由图象可知该二次函数的对称轴是( )| A. | 直线x=-1 | B. | 直线x=2 | C. | 直线x=5 | D. | 直线x=0 |
17.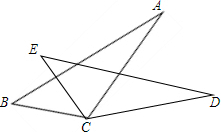 如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
 如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )
如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )| A. | AB=DE | B. | ∠B=∠E | C. | AC=DC | D. | ∠A=∠D |
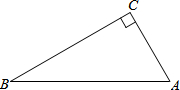 如图,在△ABC中,∠C=90°,∠A>∠B.
如图,在△ABC中,∠C=90°,∠A>∠B.
 如图,AB=AC,∠A=36°,BD是∠ABC的角平分线,求证:△ABC∽△BCD.
如图,AB=AC,∠A=36°,BD是∠ABC的角平分线,求证:△ABC∽△BCD.