题目内容
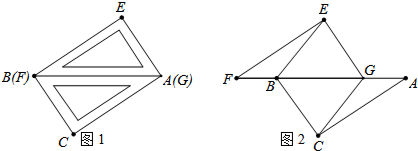
13.两块完全相同的三角板△ABC和△EFG,如图1所示放置在同一平面上(∠C=∠E=90°,∠ABC=∠EGF=60°),斜边重合.若三角板EFG不动,三角板ABC在三角板EFG所在的平面上向右滑动,图2是滑动过程中的一个位置.(1)连结BE、CG,(图2),求证:△EBF≌△CGA.
(2)三角板ABC滑动到什么位置(点B落在FG边的什么位置)时,四边形BCGE是菱形?说明理由.
分析 (1)由题意得出AB=FG,∠A=∠F=30°,AC=FE,求出AG=FB,由SAS证明△EBF≌△CGA即可;
(2)先证出EG=BG=BE,再证出BE=GC=BC,得出BE=EG=GC=BC,即可得出四边形BCGE是菱形.
解答 (1)证明:∵△ABC≌△EFG,∠C=∠E=90°,∠ABC=∠EGF=60°,
∴AB=FG,∠A=∠F=30°,AC=FE,
∵AB=FG,
∴AB-BG=FG-BG,
即AG=FB,
在△EBF和△CGA中,$\left\{\begin{array}{l}{FE=AC}&{\;}\\{∠F=∠A}&{\;}\\{FB=AG}&{\;}\end{array}\right.$,
∴△EBF≌△CGA(SAS);
(2)解:当点B落在边FG的中点时,四边形BCGE是菱形;理由如下:
∵∠E=90°,∠F=30°,
∴FG=2EG,
当B落在边FG的中点时,则FG=2BG,FG=2BE,
∴EG=BG=BE,
又∵△EBF≌△CGA,
∴BE=GC,而∠ABC=60°,
∴BE=GC=BC,
∴BE=EG=GC=BC,
∴四边形BCGE是菱形.
点评 本题考查了平移的性质、全等三角形的判定与性质、菱形的判定、等边三角形的判定;熟练掌握平移的性质和菱形的判定,并能进行推理论证是解决问题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
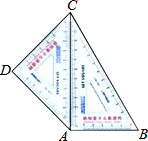 如图,学生用三角板中,等腰直角三角形三角板的斜边靠在另一个含60°角的三角形板的对边上恰好完全重合,拼成一个四边形ABCD.若60°所对的直角边长为12cm,求拼成四边形ABCD的面积.
如图,学生用三角板中,等腰直角三角形三角板的斜边靠在另一个含60°角的三角形板的对边上恰好完全重合,拼成一个四边形ABCD.若60°所对的直角边长为12cm,求拼成四边形ABCD的面积.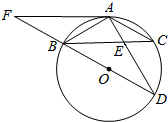 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB交⊙O的切线AF于点F,AE=2,ED=4.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB交⊙O的切线AF于点F,AE=2,ED=4.
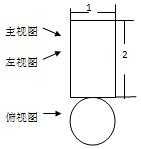 如图,长方形是一个几何体从正面看和从左面看到的形状图,圆是从上面看到的形状图(含有数据),则这个几何体的侧面展开图的面积等于( )
如图,长方形是一个几何体从正面看和从左面看到的形状图,圆是从上面看到的形状图(含有数据),则这个几何体的侧面展开图的面积等于( )