题目内容
18.(1)计算:-$\root{3}{64}$+($\frac{1}{2}$)-2-cos30°(2)解不等式组:$\left\{\begin{array}{l}{x-3(x-2)≥4}\\{\frac{2x-1}{5}<\frac{x+1}{2}}\end{array}\right.$.
分析 (1)原式第一项利用立方根定义计算,第二项利用负整数指数幂法则计算,第三项利用特殊角的三角函数值计算即可得到结果;
(2)分别求出不等式中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)原式=-4+4-$\frac{\sqrt{3}}{2}$=-$\frac{\sqrt{3}}{2}$;
(2)$\left\{\begin{array}{l}{x-3(x-2)≥4①}\\{\frac{2x-1}{5}<\frac{x+1}{2}②}\end{array}\right.$,
由①得:x≤1;
由②得:x>-7,
则不等式组的解为-7<x≤1.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
6.现一个圆心角为120°,半径为6cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),该圆锥底面圆的面积为( )
| A. | 4πcm2 | B. | 9πcm2 | C. | 16πcm2 | D. | πcm2 |
10. 如图,点S是⊙O的直径AB延长线上的一点,SC与⊙O相切于点C.若∠S=30°,则∠A等于( )
如图,点S是⊙O的直径AB延长线上的一点,SC与⊙O相切于点C.若∠S=30°,则∠A等于( )
 如图,点S是⊙O的直径AB延长线上的一点,SC与⊙O相切于点C.若∠S=30°,则∠A等于( )
如图,点S是⊙O的直径AB延长线上的一点,SC与⊙O相切于点C.若∠S=30°,则∠A等于( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
7.下列图形中,有且只有两条对称轴的图形是( )
| A. | 点 | B. | 线段 | C. | 射线 | D. | 直线 |
8.用科学记数法表示290000 0000为( )
| A. | 0.29×1010 | B. | 2.9×109 | C. | 29×108 | D. | 2.9×108 |
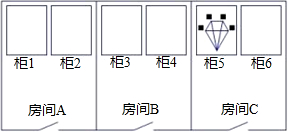 如图,有三间房,每间房内放有两个柜子,仅有一件宝物藏在某个柜子中,寻宝游戏规则如下:只允许进入三个房间中的一个房间并打开其中一个柜子即为一次游戏结束.找到宝物为游戏胜出,否则为游戏失败.
如图,有三间房,每间房内放有两个柜子,仅有一件宝物藏在某个柜子中,寻宝游戏规则如下:只允许进入三个房间中的一个房间并打开其中一个柜子即为一次游戏结束.找到宝物为游戏胜出,否则为游戏失败.