题目内容
17.如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式. 比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2 .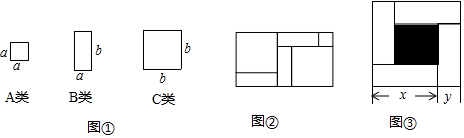
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使它的边长分别为(2a+b)、(a+2b),不画图形,试通过计算说明需要C类卡片多少张;
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使它的面积等于a2+5ab+4b2,画出这个长方形,并根据图形对多项式a2+5ab+4b2进行因式分解;
(3)如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案并判断,将正确关系式的序号填写在横线上①②③④(填写序号).
①xy=$\frac{{m}^{2}-{n}^{2}}{4}$ ②x+y=m ③x2-y2=m•n ④x2+y2=$\frac{{m}^{2}+{n}^{2}}{2}$.
分析 (1)根据多项式乘以多项式的计算法则计算即可求解;
(2)根据图形和面积公式得出即可;
(3)根据题意得出x+y=m,m2-n2=4xy,根据平方差公式和完全平方公式判断即可.
解答 解:(1)(2a+b)(a+2b)=2a2+5ab+2b2.
故需要C类卡片5张;
(2)如图所示:
a2+5ab+4b2=(a+4b)(a+b);
故答案为:(a+2b)(a+3b).
(3)根据图③得:x+y=m,
∵m2-n2=4xy,
∴xy=$\frac{{m}^{2}-{n}^{2}}{4}$,
x2-y2=(x+y)(x-y)=mn,
∴x2+y2=(x+y)2-2xy=m2-2×$\frac{{m}^{2}-{n}^{2}}{4}$=$\frac{{m}^{2}+{n}^{2}}{2}$,
∴选项①②③④都正确.
故答案为:①②③④.
点评 本题考查了因式分解的应用,长方形的面积,平方差公式,完全平方公式的应用,主要考查学生的观察图形的能力和化简能力.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
2. 如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )
如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )
 如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )
如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )| A. | 16$\sqrt{3}$ | B. | 32 | C. | 8$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
9.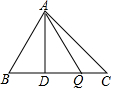 如图所示,△ABC中,已知BC=16,高AD=10,动点Q由C点沿CB向B移动(不与点B重合).设CQ长为x,△ACQ的面积为S,则S与x之间的函数关系式为( )
如图所示,△ABC中,已知BC=16,高AD=10,动点Q由C点沿CB向B移动(不与点B重合).设CQ长为x,△ACQ的面积为S,则S与x之间的函数关系式为( )
 如图所示,△ABC中,已知BC=16,高AD=10,动点Q由C点沿CB向B移动(不与点B重合).设CQ长为x,△ACQ的面积为S,则S与x之间的函数关系式为( )
如图所示,△ABC中,已知BC=16,高AD=10,动点Q由C点沿CB向B移动(不与点B重合).设CQ长为x,△ACQ的面积为S,则S与x之间的函数关系式为( )| A. | S=80-5x | B. | S=5x | C. | S=10x | D. | S=5x+80 |
6.随着信息技术的不断发展,微信已经成为人们生活中不可或缺的沟通工具,2017年2月,腾讯公司发不了《2017微信春节数据报告》,报告中显示,全国今年除夕至初五微信红包收发总量约46000000000个,把46000000000用科学记数法表示为( )
| A. | 4.6×109 | B. | 4.6×1010 | C. | 4.6×1011 | D. | 46×108 |
7.2017年某市将有5万名学生参加中考,为了解这些考生的数学成绩,中考后将从中抽取2000名考生的数学成绩进行统计分析,在这个问题中,下列说法正确的是( )
| A. | 2000名考生是总体的一个样本 | |
| B. | 每个考生是个体 | |
| C. | 这5万名考生的数学中考成绩的全体是总体 | |
| D. | 统计中采用的调查方式是普查 |
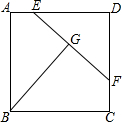 如图,正方形ABCD,点E,F分别在AD,CD上,BG⊥EF,点G为垂足,AB=5,AE=1,CF=2,则BG=$\frac{23}{5}$.
如图,正方形ABCD,点E,F分别在AD,CD上,BG⊥EF,点G为垂足,AB=5,AE=1,CF=2,则BG=$\frac{23}{5}$.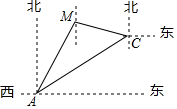 一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)