题目内容
5.先阅读,然后解方程组.解方程组
$\left\{\begin{array}{l}{x-y-1=0①}\\{4(x-y)-y=5②}\end{array}\right.$ 时,
可由 ①得x-y=1,③
然后再将③代入②得4×1-y=5,求得y=-1,
从而进一步求得$\left\{\begin{array}{l}{x=0①}\\{y=-1②}\end{array}\right.$ 这种方法被称为“整体代人法”,
请用这样的方法解下列方程组$\left\{\begin{array}{l}{2x-3y-2=0}\\{\frac{2x-3y+5}{7}+2y=9}\end{array}\right.$.
分析 仿照所给的题例先把①变形,再代入②中求出y的值,进一步求出方程组的解即可.
解答 解:$\left\{\begin{array}{l}{2x-3y-2=0①}\\{\frac{2x-3y+5}{7}+2y=9②}\end{array}\right.$,
由①得,2x-3y=2③,
代入②得$\frac{2+5}{7}$+2y=9,
解得y=4,
把y=4代入③得,2x-3×4=2,
解得x=7.
故原方程组的解为$\left\{\begin{array}{l}{x=7}\\{y=4}\end{array}\right.$.
点评 本题考查的是在解二元一次方程组时整体思想的应用,利用整体思想可简化计算.

练习册系列答案
相关题目
13.如图,P为∠AOB内一点,OC=m(m为正数),过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.C为射线OA上任一点,连结CP并延长交OB于N点

(1)若∠AOB=60°,OQ:OM:MC=1:4:2,探索CN、ON、OC之间的数量关系并加以证明.
(2)当点P在边∠AOB的平分线上运动时,问:$\frac{1}{OM}$-$\frac{1}{ON}$的值是否发生变化?如果变化,指出该值随m的变化情况;如果不变,请说明理由.
(3)在(2)的条件下,二次函数y=ax2+bx+c的x与y的部分对应值如下表:
若m的值是关于x的方程ax2+(b-1)x+c=0中较大的根,菱形OMPQ的面积为S1,△NOC的面积为S2,求$\frac{{S}_{1}}{{S}_{2}}$的取值范围.

(1)若∠AOB=60°,OQ:OM:MC=1:4:2,探索CN、ON、OC之间的数量关系并加以证明.
(2)当点P在边∠AOB的平分线上运动时,问:$\frac{1}{OM}$-$\frac{1}{ON}$的值是否发生变化?如果变化,指出该值随m的变化情况;如果不变,请说明理由.
(3)在(2)的条件下,二次函数y=ax2+bx+c的x与y的部分对应值如下表:
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -1 | 3 | 5 | 5 | … |
14.某次体育测试中,九年级一班女同学的一分钟仰卧起坐成绩(单位:个)如下表:
这此测试成绩的中位数和众数分别为( )
| 成绩 | 45 | 46 | 47 | 48 | 49 | 50 |
| 人数 | 1 | 2 | 4 | 2 | 5 | 1 |
| A. | 47,49 | B. | 48,49 | C. | 47.5,49 | D. | 48,50 |
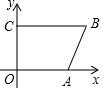 在平面直角坐标系中,A(a,0),B(12,b),C(0,b)且$\sqrt{\frac{1}{2}a-4}$+(b-6)2=0,线段PQ=7.
在平面直角坐标系中,A(a,0),B(12,b),C(0,b)且$\sqrt{\frac{1}{2}a-4}$+(b-6)2=0,线段PQ=7.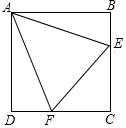 已知正方形ABCD的边长为4,点E,F分别在边BC、CD上,∠EAF=45°,若AE•AF=$\frac{40\sqrt{2}}{3}$,则EF的长为$\frac{10}{3}$.
已知正方形ABCD的边长为4,点E,F分别在边BC、CD上,∠EAF=45°,若AE•AF=$\frac{40\sqrt{2}}{3}$,则EF的长为$\frac{10}{3}$.
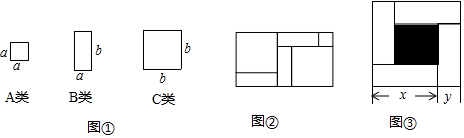
 如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点(点A在点B的左侧),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点(点A在点B的左侧),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.