题目内容
12.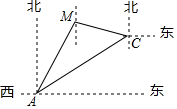 一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
分析 根据题意和特殊角的三角函数可以求得AC的长,从而可以解答本题.
解答  解:作MN⊥AC于点N,如右图所示,
解:作MN⊥AC于点N,如右图所示,
由题意可得,
∠MAC=60°-30°=30°,∠AMC=75°+30°=105°,
∴∠MCA=180°-∠MAC-∠AMC=180°-30°-105°=45°,
∵MN⊥AC,AC=40$\sqrt{2}×\frac{1}{2}=20\sqrt{2}$,
∴∠MVA=∠MNC=90°,
∴MN=NC,
设NC=a,
∴MN=a,MN=(20$\sqrt{2}-a$)•tan30°,
解得,a=$10\sqrt{6}-10\sqrt{2}$,
∴MC=$\sqrt{M{N}^{2}+N{C}^{2}}=\sqrt{2}a$=$\sqrt{2}(10\sqrt{6}-10\sqrt{2})$=$20\sqrt{3}-20$≈20×1.7-20=14(海里),
即渔船遇险M处与海岛C的距离是14海里.
点评 本题考查解直角三角形的应用-方向角问题,解答本题的关键是明确题意,找出所求问题需要的条件,画出相应的辅助线,利用锐角三角函数解答.

练习册系列答案
相关题目
1.“遇见最美春天”,某校组织九年级学生参观绿博园时,在植物园中了解到一种花瓣的花粉颗粒直径约为0.0000065米,0.0000065用科学记数法表示为( )
| A. | 6.5×10-5 | B. | 6.5×10-7 | C. | 6.5×10-6 | D. | 65×10-6 |
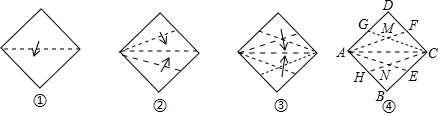
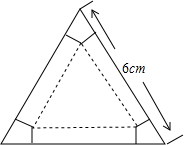 如图,有一块边长为6cm的正三角形纸板.在它的三个顶点处分剐截去一个全等的四边形,再沿图中的虚线折起,做成一个无盖的直三棱柱形纸盒,使它的侧面积等于底面积.求:
如图,有一块边长为6cm的正三角形纸板.在它的三个顶点处分剐截去一个全等的四边形,再沿图中的虚线折起,做成一个无盖的直三棱柱形纸盒,使它的侧面积等于底面积.求: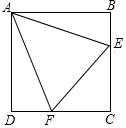 已知正方形ABCD的边长为4,点E,F分别在边BC、CD上,∠EAF=45°,若AE•AF=$\frac{40\sqrt{2}}{3}$,则EF的长为$\frac{10}{3}$.
已知正方形ABCD的边长为4,点E,F分别在边BC、CD上,∠EAF=45°,若AE•AF=$\frac{40\sqrt{2}}{3}$,则EF的长为$\frac{10}{3}$.
 已知?ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F,PE=PF=$\sqrt{3}$,EO=1,AE=3,DF=5,S?ABCD=20$\sqrt{3}$.
已知?ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F,PE=PF=$\sqrt{3}$,EO=1,AE=3,DF=5,S?ABCD=20$\sqrt{3}$.