题目内容
2. 如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )
如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=4,则矩形ABCD的面积为( )| A. | 16$\sqrt{3}$ | B. | 32 | C. | 8$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
分析 根据矩形性质得出AC=2AO,BD=2BO,AC=BD,推出AO=OB,得出等边三角形AOB,得出AC,由勾股定理求出BC,即可求出矩形ABCD的面积.
解答 解:∵四边形ABCD是矩形,
∴AC=2AO,BD=2BO,AC=BD,∠ABC=90°,
∴AO=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AC=2AO=8,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=4$\sqrt{3}$,
∴矩形ABCD的面积=AB•BC=4×4$\sqrt{3}$=16$\sqrt{3}$.
故选:A.
点评 本题考查了等边三角形的性质和判定,矩形的性质的应用,勾股定理;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
13.如图,P为∠AOB内一点,OC=m(m为正数),过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.C为射线OA上任一点,连结CP并延长交OB于N点

(1)若∠AOB=60°,OQ:OM:MC=1:4:2,探索CN、ON、OC之间的数量关系并加以证明.
(2)当点P在边∠AOB的平分线上运动时,问:$\frac{1}{OM}$-$\frac{1}{ON}$的值是否发生变化?如果变化,指出该值随m的变化情况;如果不变,请说明理由.
(3)在(2)的条件下,二次函数y=ax2+bx+c的x与y的部分对应值如下表:
若m的值是关于x的方程ax2+(b-1)x+c=0中较大的根,菱形OMPQ的面积为S1,△NOC的面积为S2,求$\frac{{S}_{1}}{{S}_{2}}$的取值范围.

(1)若∠AOB=60°,OQ:OM:MC=1:4:2,探索CN、ON、OC之间的数量关系并加以证明.
(2)当点P在边∠AOB的平分线上运动时,问:$\frac{1}{OM}$-$\frac{1}{ON}$的值是否发生变化?如果变化,指出该值随m的变化情况;如果不变,请说明理由.
(3)在(2)的条件下,二次函数y=ax2+bx+c的x与y的部分对应值如下表:
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -1 | 3 | 5 | 5 | … |
14.某次体育测试中,九年级一班女同学的一分钟仰卧起坐成绩(单位:个)如下表:
这此测试成绩的中位数和众数分别为( )
| 成绩 | 45 | 46 | 47 | 48 | 49 | 50 |
| 人数 | 1 | 2 | 4 | 2 | 5 | 1 |
| A. | 47,49 | B. | 48,49 | C. | 47.5,49 | D. | 48,50 |

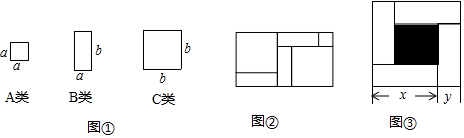
 如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张全等的等腰直角三角形纸片,面积都为2,另两张是全等的直角三角形纸片,中间一张是正方形纸片,则这个平行四边形的面积是8.
如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张全等的等腰直角三角形纸片,面积都为2,另两张是全等的直角三角形纸片,中间一张是正方形纸片,则这个平行四边形的面积是8.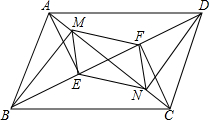 如图,已知?ABCD的对角线AC、BD交于O,AE⊥BD,CF⊥BD,BM⊥AC,DN⊥AC,E、F、M、N是垂足,连接EN、NF、FM、ME,求证:四边形MENF是平行四边形.
如图,已知?ABCD的对角线AC、BD交于O,AE⊥BD,CF⊥BD,BM⊥AC,DN⊥AC,E、F、M、N是垂足,连接EN、NF、FM、ME,求证:四边形MENF是平行四边形.