��Ŀ����
13����ͼ�٣��ڡ�ABC������BAD����CAE��ʹ��BAD=��CAE=90�㣬AB=AD��AC=AE����1����ͼ�ڣ���ͼ�ٵĻ�������ƽ���ı���ADFE��ȡBD�е�P������PF��PC���Բ���PF��PC��������ϵ��λ�ù�ϵ����˵�����ɣ�
��2����ͼ�ۣ���ͼ�ٵĻ����ϰѡ�CAE�ر�AC���ۣ���ƽ���ı���ABFE1��ȡBD�е�P������PF��PC����ͼ���а�Ҫ��ȫͼ�Σ����жϴ�ʱPF��PC��������ϵ��λ�ù�ϵ��ֱ��д�����ۣ�
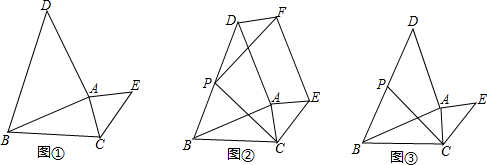
���� ��1�����ۣ�PF=PC��PF��PC����ͼ����֤��PF=PC��PF��PCֻҪ֤����PDF�ա�PAC���ɣ�
��2�����۲��䣬֤���������ƣ�1����
��� ��1�����ۣ�PF=PC��PF��PC���������£�
֤����ͼ���У�����PA��
��AB=AD����BAD=90�㣬PD=PB��
��PA=PD=PB����ADB=��ABD=��PAD=45�㣬PA��BD��
���DPA=90��
���ı���AEFD��ƽ���ı��Σ�
��DF=AE=AC��DF��AE��
���DAE+��ADF=180��
�ߡ�BAD=��CAE=90�㣬
���BAC+��DAE=180�㣬
���BAC=��ADF��
�ߡ�PDF=��ADB+��ADF=45��+��ADF��
��PAC=��PAB+��BAC=45��+��BAC��
���PDF=��PAC��
�ڡ�PDF�͡�PAC�У�
$\left\{\begin{array}{l}{PD=PA}\\{��PDF=��PAC}\\{DF=AC}\end{array}\right.$��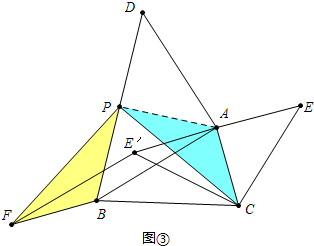
���PDF�ա�PAC��
��PF=PC����DPF=��APC��
���DPA=��FPC=90�㣬
��PF��PC��
��2�����ۣ�PF=PC��PF��PC���������£�
֤����ͼ���У�����PA��
���ı���ABFE����ƽ���ı��Σ�
��BF=AE��=AE=AC����ABF=��FE��A��FE���AB��
���FE��A=��EAB
��AB=AD����BAD=90�㣬PD=BD��
��PB=PA=PD����D=��DBA=��PAD=��PAB=45�㣬PA��BD��
���APB=90�㣬
�ߡ�PBF=��ABF-45��=��BAE-45��=��BAC+��CAE-45��=��BAC+45�㣬��PAC=��BAC+��PAB=��BAC+45�㣬
���PBF=��PAC��
�ڡ�PBF�͡�PAC�У�
$\left\{\begin{array}{l}{PB=PA}\\{��PBF=��PAC}\\{BF=AC}\end{array}\right.$��
���PBF�ա�PAC��
��PF=PC����FPB=��CPA��
���FPC=��BPA=90��
��PF��PC��
���� ���⿼��ȫ�������ε��ж������ʡ�ƽ���ı��ε����ʵ�֪ʶ����Ŀ���ѵ���ͼ���С�PDF=��PAC��֤���Լ�ͼ���С�PBF=��PAC��֤����

 ��ͼ����������ABCD�У�AB=8��Q��CD���е㣬��CD��ȡһ��P��ʹ��BAP=2��DAQ����CP�ij��ȵ��ڣ�������
��ͼ����������ABCD�У�AB=8��Q��CD���е㣬��CD��ȡһ��P��ʹ��BAP=2��DAQ����CP�ij��ȵ��ڣ�������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | $\sqrt{3}$ |
| A�� | 45�� | B�� | 90�� | C�� | 135�� | D�� | 180�� |
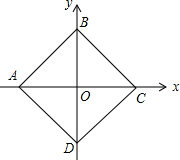 ��ͼ����ƽ��ֱ������ϵ�У��ı���ABCD�������Σ�AB=$\sqrt{2}$�����A������Ϊ��-1��0������B������Ϊ��0��1������C������Ϊ��1��0������D������Ϊ��0��-1����
��ͼ����ƽ��ֱ������ϵ�У��ı���ABCD�������Σ�AB=$\sqrt{2}$�����A������Ϊ��-1��0������B������Ϊ��0��1������C������Ϊ��1��0������D������Ϊ��0��-1����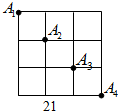 ��ͼ����A1��A2��A3��A4��ij�������ε�·���IJ��ֽ���㣬�����Ƕ�λ��ͬһ�Խ����ϣ�ij�˴ӵ�A1�������涨���һ��������ߣ���ô�����A3���߷�����6�֣�
��ͼ����A1��A2��A3��A4��ij�������ε�·���IJ��ֽ���㣬�����Ƕ�λ��ͬһ�Խ����ϣ�ij�˴ӵ�A1�������涨���һ��������ߣ���ô�����A3���߷�����6�֣�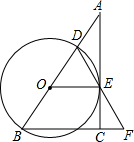 ��ͼ����Rt��ABC�У���ACB=90�㣬��D��AB���ϵ�һ�㣬��BDΪֱ������O����O��AC�Ĵ��߽�AC�ڵ�E��ǡ�ô���E�ڡ�O�ϣ�����DE���ӳ�DE��BC���ӳ����ڵ�F��
��ͼ����Rt��ABC�У���ACB=90�㣬��D��AB���ϵ�һ�㣬��BDΪֱ������O����O��AC�Ĵ��߽�AC�ڵ�E��ǡ�ô���E�ڡ�O�ϣ�����DE���ӳ�DE��BC���ӳ����ڵ�F��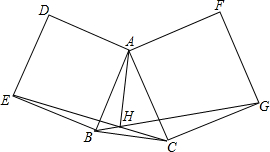 �ڡ�ABC�ı�AB��AC������������ABED��ACGF��BG��CE�ཻ��H����֤��AH��BC��
�ڡ�ABC�ı�AB��AC������������ABED��ACGF��BG��CE�ཻ��H����֤��AH��BC��