题目内容
16.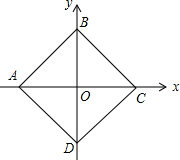 如图,在平面直角坐标系中,四边形ABCD是正方形,AB=$\sqrt{2}$,则点A的坐标为(-1,0)、点B的坐标为(0,1)、点C的坐标为(1,0)、点D的坐标为(0,-1).
如图,在平面直角坐标系中,四边形ABCD是正方形,AB=$\sqrt{2}$,则点A的坐标为(-1,0)、点B的坐标为(0,1)、点C的坐标为(1,0)、点D的坐标为(0,-1).
分析 根据正方形性质OA=OC=OB=OD,利用勾股定理求出线段OA即可.
解答 解:∵四边形ABCD是正方形,
∴OA=OC=OB=0D,
∵AB=$\sqrt{2}$,
∴OA2+OB2=AB2,
∴OA=OB=OC=OD=1,
∴点A(-1,0),点B(0,1)点C(1,0),点D(0,-1).
故答案分别为(-1,0),(0,1),(1,0),(0,-1).
点评 本题考查坐标与图形、正方形的性质、勾股定理等知识,正确利用勾股定理是解决问题的关键,属于中考常考题型.

练习册系列答案
相关题目
11.某商场计划购进A、B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
(1)若商场预计进货款为3900元,则这两种台灯各购进多少盏?
(2)若商场规定A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
| 类型 价格 | 进价(元/盏) | 售价(元/盏) |
| A型 | 30 | 55 |
| B型 | 50 | 70 |
(2)若商场规定A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
 宁波、温州两地相距约300千米,一辆火车和一辆轿车先后从宁波出发去温州,设货车行驶的时间为x(小时),如图线段OA、折线BCD分别表示货车、轿车离宁波距离y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
宁波、温州两地相距约300千米,一辆火车和一辆轿车先后从宁波出发去温州,设货车行驶的时间为x(小时),如图线段OA、折线BCD分别表示货车、轿车离宁波距离y(千米)与x(小时)之间的函数关系,根据图象解答下列问题: 小明家有一块三角形的土地,如图所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5:7:9的三部分,分别种植不同的农作物,请你设计一种方案.
小明家有一块三角形的土地,如图所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5:7:9的三部分,分别种植不同的农作物,请你设计一种方案.
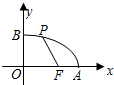 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,点F是x轴上一点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①OA=5;②AF=1;③BF=5;④OB=3.其中正确结论的序号是①③.
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,点F是x轴上一点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①OA=5;②AF=1;③BF=5;④OB=3.其中正确结论的序号是①③.