题目内容
5. 如图,在正方形ABCD中,AB=8,Q是CD的中点,在CD上取一点P,使∠BAP=2∠DAQ,则CP的长度等于( )
如图,在正方形ABCD中,AB=8,Q是CD的中点,在CD上取一点P,使∠BAP=2∠DAQ,则CP的长度等于( )| A. | 1 | B. | 2 | C. | 3 | D. | $\sqrt{3}$ |
分析 取BC的中点E,连接AE,作EF⊥AP,证明△ABE≌△AFE,得EF=BE=EC,得△EFP≌△ECP,得△ECP∽△ABE.即可求CP的长度.
解答 解:取BC的中点E,连接AE,作EF⊥AP,
则△ABE≌△ADQ,得EB=EC=4,
由$\left\{\begin{array}{l}{AE=AE}\\{∠EFA=∠EBA}\\{∠BAE=∠FAE}\end{array}\right.$,
得:△ABE≌△AFE,
∴∠AEB=∠AEF,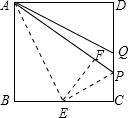
得EF=EB=EC,
∵PE=PE,
∴∠ECP=∠EFP=90°,
∴△EPC≌△EPF,
∴∠FEP=∠PEC,
∴∠AEP=∠AEF+∠FEP=90°,
∴∠PEF=∠PEC=∠EAP=∠EAB,
∴△CEP∽△BAE,
∴$\frac{PC}{EC}$=$\frac{BE}{AB}$=$\frac{4}{8}$=$\frac{1}{2}$,
即PC=2,
故选B
点评 本题考查的是全等三角形的判定,相似三角形对应边相等的性质,考查了正方形各边相等,且各内角均为直角的性质,本题求证△AEP是直角三角形是解本题的关键.

练习册系列答案
相关题目
10.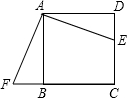 如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
 如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )| A. | 4 | B. | 8 | C. | 16 | D. | 无法计算 |
17. 如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )
如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )
 如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )
如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )| A. | 64 | B. | 16 | C. | 24 | D. | 32 |
15.为了测试某种汽车在高速路上匀速行驶的耗油量,专业测试员将汽车加满油,对汽车行驶中的情况做了记录,并把试验的数据制成如下表所示:
(1)根据上表的数据,请用x表示y,y=60-8x.
(2)若油箱中的剩余油量为20升,汽车行驶了多少小时?
(3)若该汽车贮满汽油准备从高速路出发,要匀速前往需要7小时车程的某目的地,当余油量不足5升时,油箱将会报警,请问汽车能在油箱报警之前到达目的地吗?请说明理由.
| 汽车行驶时间x(h) | 0 | 1 | 2 | 3 | … |
| 剩余油量y(L) | 60 | 52 | 44 | 36 | … |
(2)若油箱中的剩余油量为20升,汽车行驶了多少小时?
(3)若该汽车贮满汽油准备从高速路出发,要匀速前往需要7小时车程的某目的地,当余油量不足5升时,油箱将会报警,请问汽车能在油箱报警之前到达目的地吗?请说明理由.
 小明家有一块三角形的土地,如图所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5:7:9的三部分,分别种植不同的农作物,请你设计一种方案.
小明家有一块三角形的土地,如图所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5:7:9的三部分,分别种植不同的农作物,请你设计一种方案.
 如图所示,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段ME、AE、BE之间的数量关系,并说明理由.
如图所示,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段ME、AE、BE之间的数量关系,并说明理由.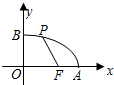 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,点F是x轴上一点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①OA=5;②AF=1;③BF=5;④OB=3.其中正确结论的序号是①③.
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,点F是x轴上一点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①OA=5;②AF=1;③BF=5;④OB=3.其中正确结论的序号是①③.