题目内容
8.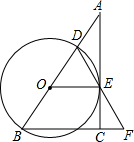 如图,在Rt△ABC中,∠ACB=90°,点D是AB边上的一点,以BD为直径作⊙O,过O作AC的垂线交AC于点E,恰好垂足E在⊙O上,连接DE并延长DE交BC的延长线于点F.
如图,在Rt△ABC中,∠ACB=90°,点D是AB边上的一点,以BD为直径作⊙O,过O作AC的垂线交AC于点E,恰好垂足E在⊙O上,连接DE并延长DE交BC的延长线于点F.(1)求证:BD=BF;
(2)若CF=2,cosB=$\frac{3}{5}$,求⊙O的半径.
分析 (1)由OE垂直于AC,BC垂直于AC,得到OE与BC平行,根据O为DB的中点,得到E为DF的中点,即OE为三角形DBF的中位线,利用中位线定理得到OE为BF的一半,再由OE为DB的一半,等量代换即可得证;
(2)在直角三角形ABC中,由cosB的值,设BC=3x,得到AB=5x,由BC+CF表示出BF,即为BD的长,再由OE为BF的一半,表示出OE,由AB-OB表示出AO,在直角三角形AOE中,利用两直线平行同位角相等得到∠AOE=∠B,得到cos∠AOE=cosB,根据cosB的值,利用锐角三角函数定义列出关于x的方程,求出方程的解得到x的值,即可求出圆的半径长.
解答 (1)证明:∵BC⊥AC,OE⊥AC
∴OE∥BC,
又∵O为DB的中点,
∴E为DF的中点,即OE为△DBF的中位线,
∴OE=$\frac{1}{2}$BF,
又∵OE=$\frac{1}{2}$BD,
则BF=BD;
(2)解:设BC=3x,根据题意得:AB=5x,
又∵CF=2,
∴BF=3x+2,
由(1)得:BD=BF,
∴BD=3x+2,
∴OE=OB=$\frac{3x+2}{2}$,AO=AB-OB=5x-$\frac{3x+2}{2}$=$\frac{7x-2}{2}$,
∵OE∥BF,
∴∠AOE=∠B,
∴cos∠AOE=cosB,即$\frac{OE}{OA}$=$\frac{3}{5}$,即$\frac{\frac{3x+2}{2}}{\frac{7x-2}{2}}$=$\frac{3}{5}$,
解得:x=$\frac{8}{3}$,
则圆O的半径为$\frac{3x+2}{2}$=5.
点评 此题考查了切线的性质,锐角三角函数定义,以及圆周角定理,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
11.某商场计划购进A、B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
(1)若商场预计进货款为3900元,则这两种台灯各购进多少盏?
(2)若商场规定A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
| 类型 价格 | 进价(元/盏) | 售价(元/盏) |
| A型 | 30 | 55 |
| B型 | 50 | 70 |
(2)若商场规定A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
17. 如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )
如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )
 如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )
如图,四边形ABCD的两条对角线互相垂直,AC+BD=16,则四边形ABCD的面积最大值是( )| A. | 64 | B. | 16 | C. | 24 | D. | 32 |
18.下列各式计算正确的是( )
| A. | 5a+a=5a2 | B. | 5a+b=5ab | C. | 5a2b-3ab2=2a2b | D. | 2ab2-5b2a=-3ab2 |
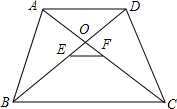 如图:在四边形ABCD中,AD∥BC,AC、BD交于点O,E、F分别是AC、BD的中点,连接E、F,求证:EF∥BC,且EF=$\frac{1}{2}$(BC-AD).
如图:在四边形ABCD中,AD∥BC,AC、BD交于点O,E、F分别是AC、BD的中点,连接E、F,求证:EF∥BC,且EF=$\frac{1}{2}$(BC-AD). 如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.
如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在CD上,连接DE,连接BG并延长交CD于点M,交DE于点H.则BH的长度为$\frac{18\sqrt{5}}{5}$.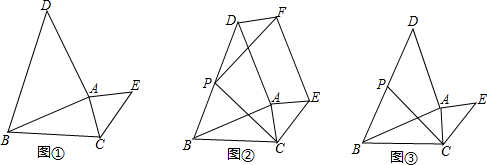
 如图所示,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段ME、AE、BE之间的数量关系,并说明理由.
如图所示,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段ME、AE、BE之间的数量关系,并说明理由.