题目内容
6.如图所示,有一个绳索拉直的木马秋千,秋千绳索AB的长度为4米,将它往前推进2米(即DE=2米),求此时秋千的绳索与静止时所夹的角度及木马上升的高度.(精确到0.1米)
分析 作CF⊥AB,由sin∠CAB=$\frac{CF}{AC}$可得∠CAB度数,根据勾股定理求得AF的长,可得BF的长度.
解答 解:过点C作CF⊥AB于点F,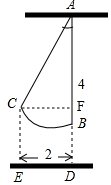
根据题意得:AB=AC=4,CF=DE=2,
在Rt△ACF中,sin∠CAB=$\frac{CF}{AC}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴∠CAB=30°,
由勾股定理可得AF2+CF2=AC2,
∴AF=$\sqrt{A{C}^{2}-C{F}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴BF=AB-AF=4-2$\sqrt{3}$≈0.5,
∴此时秋千的绳索与静止时所夹的角度为30度,木马上升的高度约为0.5米.
点评 本题主要考查勾股定理的应用及三角函数的应用,添加辅助线构建直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
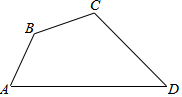 四边形ABCD中,AB=$\sqrt{6}$,BC=5-$\sqrt{3}$,CD=6,∠ABC=135°,∠BCD=120°,求AD的长.
四边形ABCD中,AB=$\sqrt{6}$,BC=5-$\sqrt{3}$,CD=6,∠ABC=135°,∠BCD=120°,求AD的长.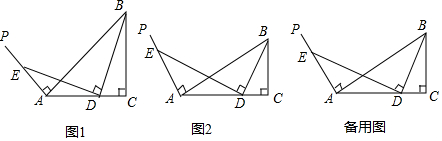
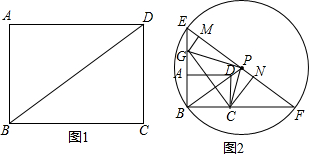
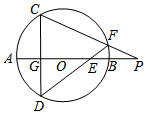 (如图)AB是⊙O的直径,弦CD⊥AB于点G,E是线段AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P,设⊙O的半径为r,求证:OE•OP=r2.
(如图)AB是⊙O的直径,弦CD⊥AB于点G,E是线段AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P,设⊙O的半径为r,求证:OE•OP=r2. 小军同学拿着边长为acm的等边三角形硬纸片从图示的位置开始在数轴上顺时针无滑动地向右滚动,当三角形的一个顶点落在x=b处时,停止滚动,且(a-1)2+|b-5|=0.
小军同学拿着边长为acm的等边三角形硬纸片从图示的位置开始在数轴上顺时针无滑动地向右滚动,当三角形的一个顶点落在x=b处时,停止滚动,且(a-1)2+|b-5|=0.