��Ŀ����
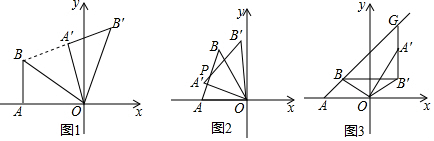
18�� С��ͬѧ���ű߳�Ϊacm�ĵȱ�������ӲֽƬ��ͼʾ��λ�ÿ�ʼ��������˳ʱ�����������ҹ������������ε�һ����������x=b��ʱ��ֹͣ�������ң�a-1��2+|b-5|=0��
С��ͬѧ���ű߳�Ϊacm�ĵȱ�������ӲֽƬ��ͼʾ��λ�ÿ�ʼ��������˳ʱ�����������ҹ������������ε�һ����������x=b��ʱ��ֹͣ�������ң�a-1��2+|b-5|=0����1����a��b��ֵ��
��2������x=b���ĵ��ǡ�ABC���ĸ����㣿˵�����ɣ�
��3��С����á�MND�ı�MN�ϵĸ�Ϊ$\frac{1}{2}$cm������MND��ÿ��3cm���ٶ��ظߵķ��������ƶ�2�룬��ʱ��MNDɨ��������Ƕ��٣�
���� ��1�����÷Ǹ��������ʼ����з������a��b��ֵ��
��2������a��b��ֵ��ȷ��AB�ij���Ȼ��������ת��������⣻
��3����MNDɨ��������ǡ�MND��������ϳ���3cm�ͱ߳���MN�ľ��ε�������ݴ˼�����⣮
��� �⣺��1�����������a-1=0��b-5=0��
���a=1��b=5��
��2������x=b���ĵ��ǡ�ABC�Ķ�����B��
��3����MND�������$\frac{\sqrt{3}}{4}$�����MNDɨ���������1��3+$\frac{\sqrt{3}}{4}$=$\frac{12+\sqrt{3}}{4}$��cm2����
���� ���⿼���˷Ǹ����������Լ�ͼ�ε���ת����ȷ�����MNDɨ����ͼ���ǹؼ���

��ϰ��ϵ�д�
�����Ŀ

 ��ͼ��Ϊ����С���ڳ��������A��B�����ľ��룬�ڳ����߶�һ��C��ʹ��BAC=90�㣬�����AC�ij�18m��BC�ij�Ϊ30m���������AB�ľ���Ϊ24m��
��ͼ��Ϊ����С���ڳ��������A��B�����ľ��룬�ڳ����߶�һ��C��ʹ��BAC=90�㣬�����AC�ij�18m��BC�ij�Ϊ30m���������AB�ľ���Ϊ24m�� ��ͼ��AD�ǵȱ�������BC���ϵĸߣ���ADΪ�����ȱ������Ρ�ADE������BE��
��ͼ��AD�ǵȱ�������BC���ϵĸߣ���ADΪ�����ȱ������Ρ�ADE������BE�� ��ͼ����·��A��B�������20km��C��DΪ����ׯ��DA��AB��A��CB��AB��B����֪DA=10km��CB=5km������Ҫ����·AB�Ͻ�һ������վE��ʹ��C��D���嵽Eվ������ȣ��ʣ�EվӦ��������A����ǧ�״���
��ͼ����·��A��B�������20km��C��DΪ����ׯ��DA��AB��A��CB��AB��B����֪DA=10km��CB=5km������Ҫ����·AB�Ͻ�һ������վE��ʹ��C��D���嵽Eվ������ȣ��ʣ�EվӦ��������A����ǧ�״���