题目内容
7.阅读下面材料后,解答提出的问题:设S=1+2+3+…+n,①
则S=n+(n-1)+(n-2)+…+1.②
由①+②,得
2S=$\underset{\underbrace{(n+1)+(n+1)+(n+1)+…+(n+1)}}{n个}$=n(n+1)
∴S=$\frac{1}{2}$n(n+1).
(1)利用上述方法或结论证明:1+3+5+…+(2n-1)=n2.
(2)若1+3+5+…+x=361,求其中的整数x.
分析 (1)设S=1+3+5+…+(2n-1)①,则S=(2n-1)+(2n-3)+(2n-5)+…+1 ②,①+②得出2S=$\underset{\underbrace{2n+2n+2n+…+2n}}{n个}$=2n2,即可得证;
(2)设x=2n-1,则1+3+5+…+2n-1=n2=361,解之得出n的值,代入x=2n-1即可.
解答 解:(1)设S=1+3+5+…+(2n-1),①
则S=(2n-1)+(2n-3)+(2n-5)+…+1,②
①+②,得:2S=$\underset{\underbrace{2n+2n+2n+…+2n}}{n个}$=2n2,
∴S=n2,即1+3+5+…+(2n-1)=n2;
(2)设x=2n-1,
则1+3+5+…+2n-1=n2=361,
解得:n=19或n=-19(舍),
∴x=2n-1=38-1=37.
点评 本题主要考查数字的变化规律及整式的运算、解方程的能力,弄清题干中求和的方法、并熟练运用是解题的关键.

练习册系列答案
相关题目
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.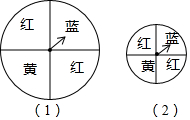 如图,两个用来摇奖的转盘,其中说法正确的是( )
如图,两个用来摇奖的转盘,其中说法正确的是( )
 如图,两个用来摇奖的转盘,其中说法正确的是( )
如图,两个用来摇奖的转盘,其中说法正确的是( )| A. | 转盘(1)中蓝色区域的面积比转盘(2)中的蓝色区域面积要大,所以摇转盘(1)比摇转盘(2)时,蓝色区域得奖的可能性大 | |
| B. | 两个转盘中指针指向蓝色区域的机会一样大 | |
| C. | 转盘(1)中,指针指向红色区域的概率是$\frac{1}{3}$ | |
| D. | 在转盘(2)中只有红、黄、蓝三种颜色,指针指向每种颜色的概率都是$\frac{1}{3}$ |
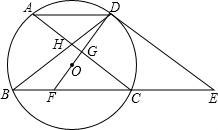 如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.
如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F.
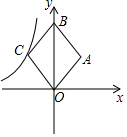 如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )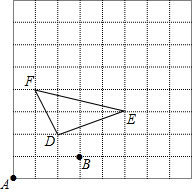 如图,用(0,0)表示A点的位置,用(3,1)表示B点的位置,那么:
如图,用(0,0)表示A点的位置,用(3,1)表示B点的位置,那么: