题目内容
12.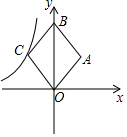 如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
分析 连接AC交OB于点D,根据菱形的性质可得出SOCD=$\frac{1}{4}$×12=3,再根据反比例函数系数k的几何意义即可求出k值,由点C在第二象限,即可确定k的值.
解答 解:连接AC交OB于点D,如图所示.
∵四边形OABC为菱形,
∴AC⊥OB,
∵菱形OABC的面积为12,
∴SOCD=$\frac{1}{4}$×12=3.
∵点C在反比例函数y=$\frac{k}{x}$的图象上,CD⊥y轴,
∴SOCD=$\frac{1}{2}$|k|=3,
解得:k=±6.
∵点C在第二象限,
∴k=-6.
故选D.
点评 本题考查了反比例函数系数k的几何以及菱形的性质,根据菱形的性质找出SOCD=$\frac{1}{4}$×12=3是解题的关键.

练习册系列答案
相关题目
2.在下列各图中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.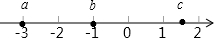 已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )
已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )
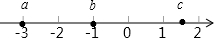 已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )
已知有理数a,b,c在数轴上的位置如图所示,则下列说法中不正确的是( )| A. | a=-3 | B. | b=-1 | C. | a的相反数为正数 | D. | c可能等于2.5 |
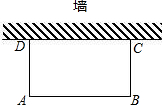 如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地,怎样围才能使矩形场地的面积为750m2?
如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地,怎样围才能使矩形场地的面积为750m2?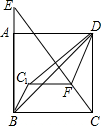 如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$.
如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$.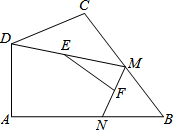 如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
如图,在四边形ABCD中,∠A=90°,AB=3,AD=$\sqrt{7}$,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( ) 如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.
如图,l1∥l2∥l3,AB=3,AD=2,DE=4,EF=7.5,求BC、BF的长.