题目内容
16.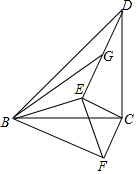 如图,在等腰直角△BCD中,∠BCD=90°,BC=CD,E为△BCD内一点,且CE⊥DE,DE=2CE,将△CDE绕点C逆时针旋转90°得到△CBF,连接EF、BE,G为DE的中点,连接BG.如果△BDG的面积为1cm2,那么BG的长度为$\sqrt{10}$cm.
如图,在等腰直角△BCD中,∠BCD=90°,BC=CD,E为△BCD内一点,且CE⊥DE,DE=2CE,将△CDE绕点C逆时针旋转90°得到△CBF,连接EF、BE,G为DE的中点,连接BG.如果△BDG的面积为1cm2,那么BG的长度为$\sqrt{10}$cm.
分析 先延长DE交BF于A,四边形AECF是正方形,设DE=2CE=2x,则AB=AF=AE=EG=x,根据△BDG的面积为1cm2,可得x的值为$\sqrt{2}$,再根据Rt△ABG中,AG=2$\sqrt{2}$,AB=$\sqrt{2}$,即可得到BG的长度.
解答 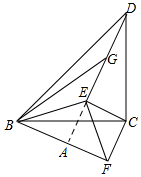 解:如图,延长DE交BF于A,
解:如图,延长DE交BF于A,
由旋转可得,△ECF是等腰直角三角形,∠BFC=∠DEC=90°=∠AEC,
∴四边形AECF是正方形,
∴CE=CF=AE=AF,
设DE=2CE=2x,则BF=2CF=2x,而G为DE的中点,
∴AB=AF=AE=EG=x,
∵AB⊥AD,△BDG的面积为1cm2,
∴$\frac{1}{2}$×DG×AB=1,即$\frac{1}{2}$x2=1,
解得x=$\sqrt{2}$,
∴Rt△ABG中,AG=2$\sqrt{2}$,AB=$\sqrt{2}$,
∴BG=$\sqrt{A{B}^{2}+A{G}^{2}}$=$\sqrt{(\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=$\sqrt{10}$,
故答案为:$\sqrt{10}$
点评 本题主要考查了旋转的性质以及等腰直角三角形的性质,解决问题的关键是作辅助线构造正方形,依据勾股定理列方程求解.

练习册系列答案
相关题目
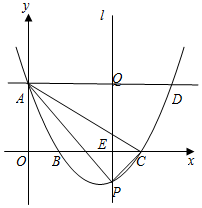 如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴交于点A(0,3),与x轴交于点B、C(B在C的左边),直线AD∥x轴交抛物线于点D,x轴上有一动点E(t,0),过点E作平行于y轴的直线l与抛物线、AD分别交于P、Q.
如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴交于点A(0,3),与x轴交于点B、C(B在C的左边),直线AD∥x轴交抛物线于点D,x轴上有一动点E(t,0),过点E作平行于y轴的直线l与抛物线、AD分别交于P、Q.
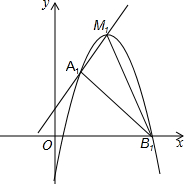 已知:抛物线Ck:y=-x2+2kx-k2+k+1(k=1,2,3…,k为正整数),抛物线Ck的顶点为Mk.
已知:抛物线Ck:y=-x2+2kx-k2+k+1(k=1,2,3…,k为正整数),抛物线Ck的顶点为Mk.