题目内容
6.证明:如果四边形的两条对角线垂直,那么依次连接它的四边中点得到一个矩形.分析 由于顺次连接四边形各边中点得到的四边形是平行四边形,再由矩形的判定可知,依次连接对角线互相垂直的四边形各边的中点所得四边形是矩形.
解答  已知在四边形ABCD中,AC⊥BD,F是AB的中点,G是BC的中点,H是DC的中点,E是AD的中点,
已知在四边形ABCD中,AC⊥BD,F是AB的中点,G是BC的中点,H是DC的中点,E是AD的中点,
求证:四边形EFGH是矩形.
证明:如图:∵E、F、G、H分别为各边中点,
∴EF∥GH∥DB,EF=GH=$\frac{1}{2}$DB,
EH=FG=$\frac{1}{2}$AC,EH∥FG∥AC,
∵DB⊥AC,
∴EF⊥EH
∴四边形EFGH是矩形.
点评 此题主要考查了矩形的判定定理,画出图形进而应用平行四边形的判定以及矩形判定是解决问题的关键.

练习册系列答案
相关题目
17.下列说法中正确的是( )
| A. | “打开电视,正在播放《动物世界》”是必然事件 | |
| B. | 某种彩票的中奖概率为$\frac{1}{1000}$,说明每买1000张彩票,一定有一张中奖 | |
| C. | 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为$\frac{1}{2}$ | |
| D. | 投掷两枚普通的正方体骰子,掷得两个6的概率是$\frac{1}{12}$ |
15.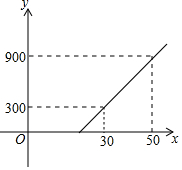 某旅客携带x(公斤)的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李质量x(公斤)的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李质量x(公斤)的对应关系,
某旅客携带x(公斤)的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李质量x(公斤)的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李质量x(公斤)的对应关系,
(1)如果旅客选择托运,求可携带的免费行李的最大质量为多少公斤?
(2)如果旅客选择快递,当1≤x≤15时,求快递费y2(元)与行李质量x(公斤)的函数关系式;
(3)某旅客携带25公斤的行李,设托运m(公斤)行李(10≤m<24,m为正整数),剩下的行李选择快递,m为何值时,总费用y的值最小,总费用的最小值是多少?
 某旅客携带x(公斤)的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李质量x(公斤)的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李质量x(公斤)的对应关系,
某旅客携带x(公斤)的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李质量x(公斤)的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李质量x(公斤)的对应关系,| 行李的质量x(公斤) | 快递费 |
| 不超过1公斤 | 10元 |
| 超过1公斤但不超过5公斤的部分 | 3元/公斤 |
| 超过5公斤但不超过15公斤的部分 | 5元/公斤 |
(2)如果旅客选择快递,当1≤x≤15时,求快递费y2(元)与行李质量x(公斤)的函数关系式;
(3)某旅客携带25公斤的行李,设托运m(公斤)行李(10≤m<24,m为正整数),剩下的行李选择快递,m为何值时,总费用y的值最小,总费用的最小值是多少?
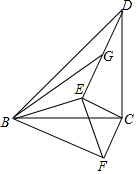 如图,在等腰直角△BCD中,∠BCD=90°,BC=CD,E为△BCD内一点,且CE⊥DE,DE=2CE,将△CDE绕点C逆时针旋转90°得到△CBF,连接EF、BE,G为DE的中点,连接BG.如果△BDG的面积为1cm2,那么BG的长度为$\sqrt{10}$cm.
如图,在等腰直角△BCD中,∠BCD=90°,BC=CD,E为△BCD内一点,且CE⊥DE,DE=2CE,将△CDE绕点C逆时针旋转90°得到△CBF,连接EF、BE,G为DE的中点,连接BG.如果△BDG的面积为1cm2,那么BG的长度为$\sqrt{10}$cm. 如图,将一副三角尺的直角顶点O重合,摆放在桌面上,若∠AOD=156°,则∠BOC=24°.
如图,将一副三角尺的直角顶点O重合,摆放在桌面上,若∠AOD=156°,则∠BOC=24°. 一只不透明的袋子中装有2个白球和一个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,小明想用树状图方法列出所有可能的结果,他正确地画出了第一次摸球的结果.
一只不透明的袋子中装有2个白球和一个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,小明想用树状图方法列出所有可能的结果,他正确地画出了第一次摸球的结果.