若a+b=$\frac{4}{3}$.ab=$\frac{1}{3}$.那么代数式a3b+ab3+2a2b2的值是$\frac{16}{27}$．题目和参考答案——青夏教育精英家教网—

题目内容

16．若a+b=$\frac{4}{3}$，ab=$\frac{1}{3}$，那么代数式a³b+ab³+2a²b²的值是$\frac{16}{27}$．

分析利用提公因式法、公式法把原式进行因式分解，代入计算即可．

解答解：a³b+ab³+2a²b²=ab（a²+2ab+b²）=ab（a+b）²，
当a+b=$\frac{4}{3}$，ab=$\frac{1}{3}$时，原式=$\frac{1}{3}$×（$\frac{4}{3}$）²=$\frac{16}{27}$，
故答案为：$\frac{16}{27}$．

点评本题考查的是因式分解的应用，掌握提公因式法、公式法因式分解的步骤是解题的关键．

练习册系列答案

相关题目

3．

如图，在平面直角坐标系中，直线y=-$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点，C为x轴正半轴上一点，S_△ABC=9．
（1）求点C的坐标；
（2）若线段AB上一点M到坐标轴的距离相等．
①求点M的坐标及直线OM的函数表达式；
②若点P为直线OM上一动点，且∠APM=∠CPM，求点P的坐标．

4．

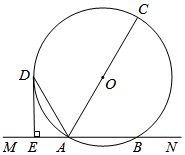如图，直线MN交⊙O于A，B两点，AC是⊙O的直径，DE与⊙O相切于点D，且DE⊥MN于点E．
求证：AD平分∠CAM．

4．设实数x，y满足x²+xy+y²=2，求x²-xy+y²的最大、最小值．

11．计算：（2a+b+1）（2a-b+1）．

1．

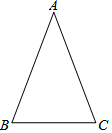定理：等腰三角形的两个底角相等（简称“等边对等角”）．
请写已知、求证，并证明．
已知：△ABC中，AB=AC，
求证：∠B=∠C．
证明：

8．已知一组等式，第1个等式：2²-1²=2+1，
                       第2个等式：3²-2²=3+2，
                       第3个等式：4²-3²=4+3．
                       …
根据上述等式的规律，第n个等式用含n的式子表示为（n+1）²-n²=n+1+n．

5．计算：2x⁵•（-x）²-（-2x²）³•（-$\frac{1}{2}$x）

6．下列方程中，属于一元二次方程的是（　　）

试题分类