题目内容
4.设实数x,y满足x2+xy+y2=2,求x2-xy+y2的最大、最小值.分析 观察可看出未知数的值没有直接给出,而是隐含在题中,需要对所求代数式进行整理然后求解.
解答 解:设x2-xy+y2=A,
∵x2+xy+y2=2,
两式相加可得,2(x2+y2)=2+A,①
两式相减得到:2xy=2-A,②
①+②×2得:2(x2+y2)+4xy=2(x+y)2=6-A≥0,
∴A≤6,
①-②×2得:2(x-y)2=3A-2≥0,
∴A≥$\frac{2}{3}$,
综上:$\frac{2}{3}$≤A≤6,即最大是6,最小值是$\frac{2}{3}$.
点评 本题考查了配方法的应用,完全平方公式,关键是设一个未知数,然后利用完全平方公式相加或相减,再根据平方数非负数的性质得出它的最大值和最小值.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
11.下列运算正确的是( )
| A. | 3a+2b=5ab | B. | -2(a-1)=-2a+1 | C. | -5x2+3x2=-2x2 | D. | a3-a2=a |
 如图,已知反比例函数y=$\frac{3}{x}$的图象与正比例函数y=kx(k>0,k≠3),y=3x的图象分别交于A,B,C,D四点.
如图,已知反比例函数y=$\frac{3}{x}$的图象与正比例函数y=kx(k>0,k≠3),y=3x的图象分别交于A,B,C,D四点.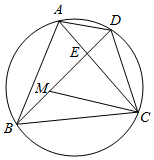 如图,点D是等边三角形ABC外接圆上一点.M是BD上一点,且满足DM=DC,点E是AC与BD的交点.
如图,点D是等边三角形ABC外接圆上一点.M是BD上一点,且满足DM=DC,点E是AC与BD的交点.