题目内容
3. 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,C为x轴正半轴上一点,S△ABC=9.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,C为x轴正半轴上一点,S△ABC=9.(1)求点C的坐标;
(2)若线段AB上一点M到坐标轴的距离相等.
①求点M的坐标及直线OM的函数表达式;
②若点P为直线OM上一动点,且∠APM=∠CPM,求点P的坐标.
分析 (1)由题意可得A(-4,0),B(0,-3),设C(m,0),由S△ABC=9,可得方程$\frac{1}{2}$•(4+m)×3=9,解方程即可.
(2)①由题意可知,OM是一、三象限的角平分线,所以直线OM的解析式为y=x,列出方程组解方程组即可求出点M坐标.
②设点P(m,m),作OE⊥AP于E,OF⊥PC于F.由$\frac{{S}_{△PAO}}{{S}_{△POC}}$=$\frac{\frac{1}{2}•PA•OE}{\frac{1}{2}•PC•OF}$=$\frac{OA}{OC}$,因为∠APM=∠CPM,OE⊥AP于E,OF⊥PC于F,可得OE=OF,所以$\frac{PA}{PC}$=$\frac{OA}{OC}$=2,所以PA=2PC,所以PA2=4•PC2,由此可得方程(m+4)2+m2=4[(m-2)2+m2],解方程即可.
解答 解:(1)∵直线y=-$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,
∴可得A(-4,0),B(0,-3),设C(m,0),
由题意$\frac{1}{2}$•(4+m)×3=9,
∴m=2,
∴点C坐标为(2,0).
(2)①点M到坐标轴的距离相等,
∴OM是一、三象限的角平分线,
∴直线OM的解析式为y=x,
由$\left\{\begin{array}{l}{y=x}\\{y=-\frac{3}{4}x-3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{12}{7}}\\{y=-\frac{12}{7}}\end{array}\right.$,
∴点M坐标为(-$\frac{12}{7}$,-$\frac{12}{7}$).
② 如图,设点P(m,m),作OE⊥AP于E,OF⊥PC于F.
如图,设点P(m,m),作OE⊥AP于E,OF⊥PC于F.
∵$\frac{{S}_{△PAO}}{{S}_{△POC}}$=$\frac{\frac{1}{2}•PA•OE}{\frac{1}{2}•PC•OF}$=$\frac{OA}{OC}$,
又∵∠APM=∠CPM,OE⊥AP于E,OF⊥PC于F.
∴OE=OF,
∴$\frac{PA}{PC}$=$\frac{OA}{OC}$=2,
∴PA=2PC,
∴PA2=4•PC2,
∴(m+4)2+m2=4[(m-2)2+m2],
∴m=4或0(舍弃),
∴点P的坐标为(4,4).
点评 本题考查一次函数综合题、角平分线的性质定理、两点间距离公式等知识,解题的关键是学会构建一次函数,利用方程组求两个函数的交点坐标,学会用方程的思想思考问题,所以中考压轴题.

| A. | 3a+2b=5ab | B. | -2(a-1)=-2a+1 | C. | -5x2+3x2=-2x2 | D. | a3-a2=a |
 如图,在⊙O中,∠AOB=62°,则∠ACB=31度.
如图,在⊙O中,∠AOB=62°,则∠ACB=31度. 如图,O为直线BE上的一点,∠AOE=36°,OC平分∠AOB,OD平分∠BOC,求∠AOD的度数.
如图,O为直线BE上的一点,∠AOE=36°,OC平分∠AOB,OD平分∠BOC,求∠AOD的度数.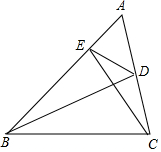 如图,在△ABC中,点D、E分别在边AC,AB上,∠ABD=∠ACE,连接DE,求证△ADE∽△ABC.
如图,在△ABC中,点D、E分别在边AC,AB上,∠ABD=∠ACE,连接DE,求证△ADE∽△ABC. 如图,已知反比例函数y=$\frac{3}{x}$的图象与正比例函数y=kx(k>0,k≠3),y=3x的图象分别交于A,B,C,D四点.
如图,已知反比例函数y=$\frac{3}{x}$的图象与正比例函数y=kx(k>0,k≠3),y=3x的图象分别交于A,B,C,D四点.