题目内容
8.已知一组等式,第1个等式:22-12=2+1,第2个等式:32-22=3+2,
第3个等式:42-32=4+3.
…
根据上述等式的规律,第n个等式用含n的式子表示为(n+1)2-n2=n+1+n.
分析 观察前3个等式可知2=1+1、3=2+1、4=3+1,结合等式的变化即可得出第n个等式为(n+1)2-n2=n+1+n,此题得解.
解答 解:∵2=1+1,3=2+1,4=3+1,…,
∴第n个等式用含n的式子表示为:(n+1)2-n2=n+1+n.
故答案为:(n+1)2-n2=n+1+n.
点评 本题考查了规律型中数字的变化类,根据等式中数的变化找出变化规律是解题的关键.

练习册系列答案
相关题目
20.公园门票价格规定如表:
某学校七年级(1)、(2)两个班共104人去游公园,其中(1)班人数较少,多于4人,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)两班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游公园,作为组织者的你将如何购票才能省钱?省多少?
| 购票张数 | 1-50张 | 51~100张 | 100张以上 |
| 每张票价 | 13元 | 11元 | 9元 |
(1)两班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游公园,作为组织者的你将如何购票才能省钱?省多少?
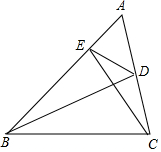 如图,在△ABC中,点D、E分别在边AC,AB上,∠ABD=∠ACE,连接DE,求证△ADE∽△ABC.
如图,在△ABC中,点D、E分别在边AC,AB上,∠ABD=∠ACE,连接DE,求证△ADE∽△ABC.