题目内容
11. 如图,在四边形ABCD中,AB=8,BC=6,∠B=90°,AD=CD=5$\sqrt{2}$,求四边形ABCD的面积.
如图,在四边形ABCD中,AB=8,BC=6,∠B=90°,AD=CD=5$\sqrt{2}$,求四边形ABCD的面积.
分析 连接AC,在Rt△ABC中根据勾股定理求出AC的长,再由勾股定理的逆定理判断出△ADC是直角三角形,根据S四边形ABCD=S△ABC+S△ACD即可得出结论.
解答 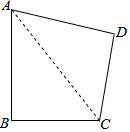 解:连接AC,在Rt△ABC中,
解:连接AC,在Rt△ABC中,
∵AB=8,BC=6,∠B=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10.
在△ADC中,∵AD=CD=5$\sqrt{2}$,
∴AD2+CD2=(5$\sqrt{2}$)2+(5$\sqrt{2}$)2=100.
∵AC2=102=100,
∴AD2+CD2=AC2,
∴∠ADC=90°,
∴S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}$AB•BC+$\frac{1}{2}$AD•DC=$\frac{1}{2}$×8×6+$\frac{1}{2}$×5$\sqrt{2}$×5$\sqrt{2}$=24+25=49.
点评 本题考查的是勾股定理及勾股定理的逆定理,不规则几何图形的面积,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
13.使式子$\frac{x+3}{x-3}$÷$\frac{x+5}{x-4}$有意义的x值是( )
| A. | x≠3,且x≠-5 | B. | x≠3,且x≠4 | C. | x≠4且 x≠-5 | D. | x≠3,且x≠4且x≠-5 |
6. 如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,得OP2016的值等于( )
如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,得OP2016的值等于( )
 如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,得OP2016的值等于( )
如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,得OP2016的值等于( )| A. | $\sqrt{2014}$ | B. | $\sqrt{2015}$ | C. | $\sqrt{2016}$ | D. | $\sqrt{2017}$ |
3.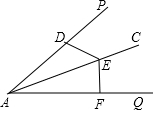 如图,已知AC平分∠PAQ,D、E、F分别是AP、AC、AQ上的三个动点,下列说法不正确的是( )
如图,已知AC平分∠PAQ,D、E、F分别是AP、AC、AQ上的三个动点,下列说法不正确的是( )
 如图,已知AC平分∠PAQ,D、E、F分别是AP、AC、AQ上的三个动点,下列说法不正确的是( )
如图,已知AC平分∠PAQ,D、E、F分别是AP、AC、AQ上的三个动点,下列说法不正确的是( )| A. | DE⊥AP,EF⊥AQ,可推出AD=AF | B. | 若DE=EF,可推出AD=AF | ||
| C. | 若∠DEA=∠FEA,可推出AD=AF | D. | 若∠ADE=∠AFE,可推出AD=AF |
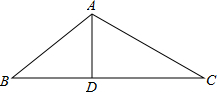 如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.
如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.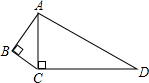 如图,∠B=∠ACD=90°,BC=3,AB=4,CD=12,则AD=13.
如图,∠B=∠ACD=90°,BC=3,AB=4,CD=12,则AD=13.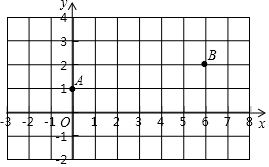 如图,在平面直角坐标系xOy中,已知点A(0,1),B(6,2),在x轴上找一点P,使得PA+PB最小,则点P的坐标是(4,0),此时△PAB的面积是2.
如图,在平面直角坐标系xOy中,已知点A(0,1),B(6,2),在x轴上找一点P,使得PA+PB最小,则点P的坐标是(4,0),此时△PAB的面积是2.