题目内容
14.已知一个直角三角形的面积为84cm2,其中一条直角边的长为7cm,则该直角三角形的斜边的长为( )| A. | 23cm | B. | 24cm | C. | 25cm | D. | 26cm |
分析 设另一条直角边的长为xcm,根据三角形的面积公式求出x的值,由勾股定理即可得出斜边长.
解答 解:设另一条直角边的长为xcm,
∵直角三角形的面积为84cm2,其中一条直角边的长为7cm,
∴$\frac{1}{2}$×7x=84,解得x=24(cm),
∴该直角三角形的斜边的长=$\sqrt{{7}^{2}+2{4}^{2}}$=25(cm).
故选C.
点评 本题考查的是勾股定理和三角形的面积公式,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
16.亮亮做抛硬币的实验,共抛了10次,3次正面朝上,7次反面朝上,准确的说法是( )
| A. | 正面朝上的频数是3 | B. | 正面朝上的频率是3 | ||
| C. | 反面朝上的频率是7 | D. | 正面朝上的频数是0.3 |
6. 如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,得OP2016的值等于( )
如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,得OP2016的值等于( )
 如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,得OP2016的值等于( )
如图,OP=1,过P作PP1⊥OP,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,得OP2016的值等于( )| A. | $\sqrt{2014}$ | B. | $\sqrt{2015}$ | C. | $\sqrt{2016}$ | D. | $\sqrt{2017}$ |
3.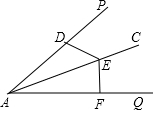 如图,已知AC平分∠PAQ,D、E、F分别是AP、AC、AQ上的三个动点,下列说法不正确的是( )
如图,已知AC平分∠PAQ,D、E、F分别是AP、AC、AQ上的三个动点,下列说法不正确的是( )
 如图,已知AC平分∠PAQ,D、E、F分别是AP、AC、AQ上的三个动点,下列说法不正确的是( )
如图,已知AC平分∠PAQ,D、E、F分别是AP、AC、AQ上的三个动点,下列说法不正确的是( )| A. | DE⊥AP,EF⊥AQ,可推出AD=AF | B. | 若DE=EF,可推出AD=AF | ||
| C. | 若∠DEA=∠FEA,可推出AD=AF | D. | 若∠ADE=∠AFE,可推出AD=AF |
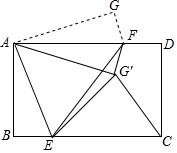 如图所示,矩形纸片ABCD中,AB=6,CB=8,现将纸片折叠压平,使A,C两点重合,折痕为EF,点D的对应点为G,再将△AGF沿着AF翻折,得△AG′F,连接EG′和CG′,则△EG′C的面积是$\frac{43}{4}$.
如图所示,矩形纸片ABCD中,AB=6,CB=8,现将纸片折叠压平,使A,C两点重合,折痕为EF,点D的对应点为G,再将△AGF沿着AF翻折,得△AG′F,连接EG′和CG′,则△EG′C的面积是$\frac{43}{4}$.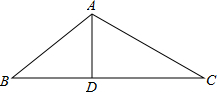 如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.
如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.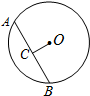 如图,在⊙O中,点C是AB的中点,AB=4cm,OC=1cm,则OB的长是$\sqrt{5}$cm.
如图,在⊙O中,点C是AB的中点,AB=4cm,OC=1cm,则OB的长是$\sqrt{5}$cm.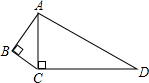 如图,∠B=∠ACD=90°,BC=3,AB=4,CD=12,则AD=13.
如图,∠B=∠ACD=90°,BC=3,AB=4,CD=12,则AD=13.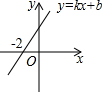 如图,一次函数y=kx+b的图象与x轴的交点坐标为(-2,0),则下列说法:
如图,一次函数y=kx+b的图象与x轴的交点坐标为(-2,0),则下列说法: