题目内容

19．计算（0.5）2003•（-2）2002的结果是（　　）
A．-0.5B．0.5C．1D．2

分析 利用积的乘方得到原式=[0.5×（-2）]2002•0.5，然后进行乘方运算即可．

解答 解：原式=[0.5×（-2）]2002•0.5
=1×0.5
=0.5．
故选B．

点评 本题考查了幂的乘方与积的乘方：幂的乘方法则：底数不变，指数相乘，即（am）n=amn（m，n是正整数）；积的乘方法则：把每一个因式分别乘方，再把所得的幂相乘，即（ab）n=anbn（n是正整数）．

练习册系列答案
相关题目
2．计算
（1）$\sqrt{24}$+$\sqrt{54}$+$\sqrt{6}$          
 （2）（$\sqrt{2}$+1）2017（$\sqrt{2}$-1）2016．
10．关于x的一元二次方程x2-3x-k2=0（k是常数）的根的情况是（　　）
A．有两个不相等的实数根B．有两个相等的实数根
C．没有实数根D．方程根的情况与k的取值有关
7．先观察表格，再解决问题．
项数第一项前两项前三项前四项前五项
式子①11+21+2+31+2+3+41+2+3+4+5
式子②1212+2212+22+3212+22+32+4212+22+32+42+52
两个式子的比1$\frac{3}{5}$$\frac{3}{7}$$\frac{1}{3}$$\frac{3}{11}$
（1）1+2+3+4+5+…+40=820（直接写出结果）；
（2）计算12+22+32+42+…+402的值；
（3）计算22+42+62+82+…+402的值．
14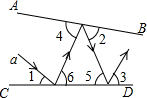．光线a照射到平面镜CD上，然后在平面镜AB和CD之间来回反射，光线的反射角等于入射角．若已知∠1=25°，∠3=75°，则∠2=（　　）
A．40°B．45°C．50°D．55°
4．如图1所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地．两车同时出发，匀速行驶．图2是客车、货车离C站的路程y1，y2（千米）与行驶时间x（小时）之间的函数关系图象．

（1）填空：A，B两地相距440千米；
（2）求两小时后，货车离C站的路程y2与行驶时间x之间的函数关系式；
（3）当客车行驶多长时间，客、货两车相距150千米．
11．解方程组：
①$\left\{\begin{array}{l}{\frac{x+1}{5}-\frac{y-1}{2}=-1}\\{x+y=2}\end{array}\right.$；
 ②$\left\{\begin{array}{l}{\frac{y}{3}-\frac{x+1}{6}=3}\\{2（x-\frac{y}{2}）=3（x+\frac{y}{18}）}\end{array}\right.$； 
 ③$\left\{\begin{array}{l}{x+y+z=2}\\{x-y+z=0}\\{x-z=4}\end{array}\right.$．
8．解下列不等式或不等式组，并把解集在数轴上表示出来
（1）2x＜5x-6                          
（2）3x+3≥5x-5
（3）10-4（x-3）≤2（x-1）
（4）3（x+3）＜5（x-1）+7
（5）$\frac{3（x+1）}{8}$-1＞$\frac{x-5}{2}$-x　         　
（6）$\frac{2x-1}{4}$-$\frac{5x+2}{6}$≤-1．
9．数1+$\sqrt{2}$的相反数是-1-$\sqrt{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网