题目内容
4.如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.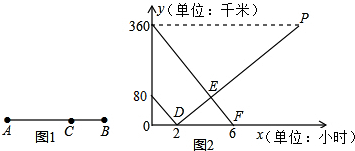
(1)填空:A,B两地相距440千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)当客车行驶多长时间,客、货两车相距150千米.
分析 (1)根据图象中的数据即可得到A,B两地的距离;
(2)根据函数图象中的数据即可得到两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)根据题意可以分相遇前和相遇后两种情况进行解答.
解答 解:(1)由函数图象可得,
A,B两地相距:80+360=440(千米),
故答案为:440;
(2)设两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式是y2=kx+b,
由图象可知,货车的速度为:80÷2=40千米/时,
∴货车到达A的时间为:440÷40=11(小时),
∴点P的坐标为(11,360),
∴$\left\{\begin{array}{l}{2k+b=0}\\{11k+b=360}\end{array}\right.$,得$\left\{\begin{array}{l}{k=40}\\{b=-80}\end{array}\right.$,
即两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式是y2=40x-80;
(3)由题意可得,
相遇前两车相距150千米用的时间为:(440-150)÷(80÷2+360÷6)=2.9(小时),
相遇后两车相距150千米用的时间为:2.9+(150×2)÷(80÷2+360÷6)=2.9+300÷100=5.9(小时),
当客车行驶2.9小时或5.9小时时,客、货两车相距150千米.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想和函数的思想解答.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
7. 如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )
如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )
 如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )
如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )| A. | 25cm | B. | 50cm | C. | 75cm | D. | 100cm |
19.计算(0.5)2003•(-2)2002的结果是( )
| A. | -0.5 | B. | 0.5 | C. | 1 | D. | 2 |
9.有一个两位数,它的十位数字与个位数字之和为5,则符合条件的两位数有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
16.下列各组数中,成比例的是( )
| A. | 7,5,14,5 | B. | 6,8,3,4 | C. | 3,5,9,12 | D. | 2,3,6,12 |
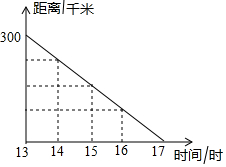 某客运汽车下午运行时距终点的距离与运行时间关系如图所示,13:00汽车距终点300千米,汽车于17时到达终点.
某客运汽车下午运行时距终点的距离与运行时间关系如图所示,13:00汽车距终点300千米,汽车于17时到达终点.