题目内容
7.先观察表格,再解决问题.| 项数 | 第一项 | 前两项 | 前三项 | 前四项 | 前五项 | |
| 式子① | 1 | 1+2 | 1+2+3 | 1+2+3+4 | 1+2+3+4+5 | |
| 式子② | 12 | 12+22 | 12+22+32 | 12+22+32+42 | 12+22+32+42+52 | |
| 两个式子的比 | 1 | $\frac{3}{5}$ | $\frac{3}{7}$ | $\frac{1}{3}$ | $\frac{3}{11}$ |
(2)计算12+22+32+42+…+402的值;
(3)计算22+42+62+82+…+402的值.
分析 (1)这是一个等差数列,根据高斯求和公式直接求出即可;
(2)观察表格的规律,式子①与式子②的比值通式为$\frac{3}{2n+1}$,根据(1)和这个通式即可求得结论;
(3)把22+42+62+82+…+402化为22×(12+22+32+42+…+202),根据(2)即可求得结论.
解答 解:(1)1+2+3+4+5+…+40=$\frac{1}{2}$(1+40)×40=820,
故答案为:420;
(2)12+22+32+42+…+402=$\frac{81}{3}$×(1+2+3+4+5+…+40)=$\frac{81}{3}$×820=22140;
(3)1+2+3+4+5+…+20=$\frac{1}{2}$×(1+20)×20=210
12+22+32+42+…+202=$\frac{41}{3}$×(1+2+3+4+5+…+20)=$\frac{41}{3}$×210=2870,
22+42+62+82+…+402=22×(12+22+32+42+…+202)=4×2870=11480.
点评 本题主要考查了等差数列,数字的变化,能根据表格的规律,得到式子①与式子②的比值通式为$\frac{3}{2n+1}$是解题的关键.

练习册系列答案
相关题目
11.下列图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.计算(0.5)2003•(-2)2002的结果是( )
| A. | -0.5 | B. | 0.5 | C. | 1 | D. | 2 |
16.下列各组数中,成比例的是( )
| A. | 7,5,14,5 | B. | 6,8,3,4 | C. | 3,5,9,12 | D. | 2,3,6,12 |
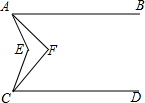 如图,已知AB∥CD,∠EAF$\frac{1}{4}$4∠EAB,∠ECF=$\frac{1}{4}$∠ECD,已知∠AEC=72°,则∠AFC=54°.
如图,已知AB∥CD,∠EAF$\frac{1}{4}$4∠EAB,∠ECF=$\frac{1}{4}$∠ECD,已知∠AEC=72°,则∠AFC=54°.